Kirill Andreev, D.Jdanov, E.Soroko, and V.Shkolnikov
Revised: December 16, 2003
1. Introduction
3.1 Splitting 1x1 death counts into Lexis triangles
3.2 Splitting death counts in open age intervals into Lexis triangles
6. Computations of period life tables by cohort method
Life tables for countries with data available for ages 80-99 only
Period life tables for aggregates of countries
The Kannisto-Thatcher database (K-T database) includes data on death counts and population counts classified by sex, year of age, year of birth, and calendar year for more than 30 countries. The database was established for the estimation of death rates at the highest ages (above age 80). The core set of data was assembled, tested for quality, and converted into cohort mortality histories by Väinö Kannisto, former United Nations advisor on demographic and social statistics. Comparable materials on England and Wales were made available by A. Roger Thatcher, former Director of the Office of Population Censuses and Surveys and Registrar-General of England and Wales. With research funding provided by the U.S. National Institute on Aging and the Danish Research Councils, the Kannisto and Thatcher data bases were computerized at the Aging Research Unit of the Centre for Health and Social Policy at Odense University Medical School in 1993 under the supervision of James W. Vaupel. Currently, the Max Planck Institute for Demographic Research, Germany, maintains the database.
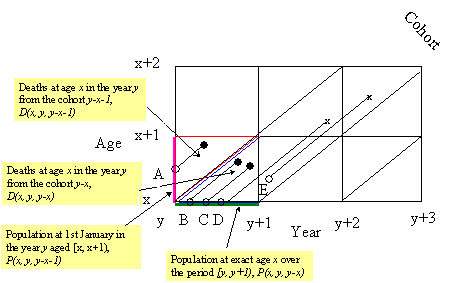
The database structure is strongly tied to the concept of the Lexis diagram. A Lexis diagram is an important descriptive device frequently used in demography and epidemiology. It usually pertains to a particular population, e.g. Danish females, and represents individual lives by line segments joining the moment of entering and leaving the population (Figure 2.1).
Figure 2.1. Illustration of a population opened for migration, using the Lexis diagram.

Figure 2.1 shows an example of the Lexis diagram starting with age x and year y and covering 2 years of age and 3 years of time. In this particular example, the entire population consists only of five individuals: A, B, C, D, and F. Hollow circles show the moments of individuals entering the population, filled circles and crosses x show the moments of leaving the population. As the event of interest is the death of an individual, we distinguish between leaving the population due to death (filled circle) or due to other reasons (cross x). In the demographic data, later usually represents immigration. Consider, for example, individual A. At the beginning of year y he was aged approximately x+0.5. He died during the same year y just before celebrating his birthday x+1. Another example is individual E for whom no time of death is recorded: he entered the population in the year y+1 and moved out in the year y+2.
Individual data of this kind usually are not available from vital statistics. Instead, various aggregates of individual data are published. In the countries with advanced statistical systems, e.g. Denmark, population and death counts are classified according to the current year, age and cohort, which uniquely define an elementary triangle on the Lexis diagram. Throughout this text we will use D to denote death counts and P for population estimates. Thus, D(x, y, y-x) is the number of deaths at age x, in the year y and from cohort y-x (this quantity can be obtained by counting filled circles in the red triangle in Figure 2.1) and D(x, y, y-x-1) is the number of deaths at age x, in the year y and from cohort y-x-1 (blue triangle in Figure 2.1). Population estimates can be derived from a count of life span lines crossing either horizontal or vertical segments of the Lexis diagram. For example, P(x, y, y-x-1) is the number of individuals aged [x, x+1) on January, 1st in the year y (magenta line in Figure 1). P(x, y, y-x) is a population that reached the exact age x during the period [y, y+1).
The basic assumption of the K-T database is that it is closed for migration. Due to the fact that the database is covering ages above 80 only, such assumption seems to be reasonable and allows us to employ extinct generation method for producing population estimates. Thus, individuals D and E in Figure 2.1 are impossible cases for the closed population and the figure can be simplified as follows (Fig. 2.2).
Figure 2.2 Illustration of a population closed for migration, with a Lexis diagram.
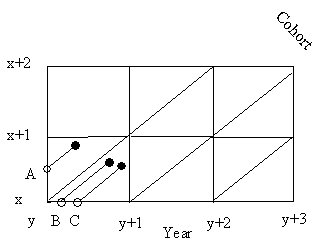
Figure 2.2 is a modification of Figure 2.1 showing three individuals, who died in the age-year domain covered by the Lexis diagram. As before, an elementary element of the Lexis diagram is a triangle. The K-T database was designed in a way to accommodate data at such level of details. For each country data are stored in different files for males and females and refer to a particular age-year domain of the Lexis diagram. Each record in the database stores data for one Lexis triangle, and it includes the following columns:
|
YEAR |
AGE |
TRIANGLE |
COHORT |
POPULATION |
DEATHS |
where
YEAR - current year y;
AGE - current age x;
COHORT - year of birth z;
TRIANGLE - Lexis triangle number. This variable has value 1 if z = y - x and value 2 if z = y - x - 1;
POPULATION - population estimates P(x, y, y-x-1) on January, 1st in year y aged [x,x+1) or population estimates P(x, y, y-x) at the exact age x during period [y,y+1);
DEATHS - number of deaths in the Lexis triangle D(x, y, y-x) or D(x, y, y-x-1);
We can see that the database includes four 'dimensional' variables (YEAR, AGE, TRIANGLE and COHORT) and two 'information' variables (POPULATION and DEATHS). Please note that only three 'dimensional' variables define the location of a Lexis triangle on the Lexis diagram and that there is a simple relation between them:
COHORT + AGE + TRIANGLE - 1 = YEAR
Numeric computations and data retrieval can be significantly faster and easier to perform if certain constraints on the data structure are imposed. In the K-T database the data are sorted in ascending order by YEAR, AGE and TRIANGLE, each year includes the same number of ages, and each age includes two Lexis triangles. In this case database record r (the first record has index 1) storing data for the Lexis triangle defined by age x, year y and triangle g is equal to
where y1 denotes the first year covered by the database, and x1 and x2 the first and last ages. Equation 2.1 is crucial for the fast retrieval of data from the database and for numeric manipulation with data.
The years and ages covered by a particular database ![]() are
specific to that population. The starting age x1 is always
80. The highest age x2 is selected to be higher than the maximum
age at death or the maximum age of survival attained in this population. Usually,
it is 5 or 10 years higher than the maximum age for simplifying the updating process.
are
specific to that population. The starting age x1 is always
80. The highest age x2 is selected to be higher than the maximum
age at death or the maximum age of survival attained in this population. Usually,
it is 5 or 10 years higher than the maximum age for simplifying the updating process.
For illustration, we will construct a Lexis database from the individual data given in Figure 2.2. Let us assume that x = 80 and y = 1950. The YEAR variable has values from 1950 to 1953 and the AGE variable has values from 80 to 81. By counting population and death counts in Lexis triangles, the following database is constructed:
|
Year |
Age |
Triangle |
Cohort |
Population |
Deaths |
|
1950 |
80 |
1 |
1870 |
2 |
2 |
|
1950 |
80 |
2 |
1869 |
1 |
1 |
|
1950 |
81 |
1 |
1869 |
0 |
0 |
|
1950 |
81 |
2 |
1868 |
0 |
0 |
|
1951 |
80 |
1 |
1871 |
0 |
0 |
|
1951 |
80 |
2 |
1870 |
0 |
0 |
|
1951 |
81 |
1 |
1870 |
0 |
0 |
|
1951 |
81 |
2 |
1869 |
0 |
0 |
|
1952 |
80 |
1 |
1872 |
0 |
0 |
|
1952 |
80 |
2 |
1871 |
0 |
0 |
|
1952 |
81 |
1 |
1871 |
0 |
0 |
|
1952 |
81 |
2 |
1870 |
0 |
0 |
The first record in this database corresponds to the Lexis triangle (year = 1950, age = 80 and triangle = 1) with two deaths and the population at risk 2. The second record in the database corresponds to the Lexis triangle (year = 1950, age = 80 and triangle = 2) with one death and the population on 1st January 1950 at age 80 being one. For all other Lexis triangles, deaths and population are zeros.
3.1 Splitting 1x1 death counts into Lexis triangles
For many countries and especially for earlier years, death counts are not available by Lexis triangles. Therefore, deaths in each Lexis triangle need to be estimated before they can be added to the database. Currently, we are using simple 50/50 splitting for all possible death aggregates.
If deaths D(x, y) are given by a single year and age (on the Lexis diagram this area appears as rectangle), then
![]()
At high ages as shown by several studies (cf. e.g. Vallin, 1973) in the real
data deaths occurred from the older cohort![]() are in fact 1 or 2% higher than deaths
are in fact 1 or 2% higher than deaths ![]() occurred from the younger cohort. This is due to: a) steep
increase of death rates at ages 80 and over, and, b) the fact that the average age at death in
the Lexis triangle corresponding to the younger cohort is half of the year higher.
occurred from the younger cohort. This is due to: a) steep
increase of death rates at ages 80 and over, and, b) the fact that the average age at death in
the Lexis triangle corresponding to the younger cohort is half of the year higher.
If deaths D(y,z) are given by a single year and cohort (on the Lexis diagram this area appears as vertical parallelogram), we use a simple 50/50 splitting.
If death counts are aggregated by broader age categories, i.e. by 5-year age groups, or if they are given for an opened age interval, i.e. for 100 years of age and over, they are not incorporated in the K-T database. In the latter case, for example, we will include only data up to age 99.
Non-integer death or population numbers are not accepted in the K-T database. If for a given rectangle or a vertical trapezoid the death count has an odd number (2n+1), then (n+1) death is to be added to the lower triangle and n to the upper triangle.
3.2 Splitting death counts in open age intervals into Lexis triangles
In many countries deaths at the highest ages are published as a total number of deaths in an opened age group. For estimating the mortality surface over age and time they have to be split by single year of age and by cohort. An application of the many methods of the present Methodology requires these detailed categories.
This problem is encountered almost invariably in historical data but it is also common in contemporary death tabulations. Many national statistical offices do not rely on the quality of death counts and age-at-death data at very high ages; therefore they never publish such data. Other national statistical offices, i.e. Statistics Canada, intentionally the restrict publication of detailed data due to reason of confidentiality. Some statistical offices provide detailed or less detailed data depending on the time period. Australian deaths for the year 2000, for example, have been published by 5-year age groups with 100+ open age group.
The method for splitting deaths in open age group relies on the assumption that deaths in the current year occurred in a stationary population with an age-specific pattern of death rates following the Kannisto mortality model (Thatcher, 1999).
Let D(xi) be the number of deaths in age group [xi, xi+1), i=1,...,n-1. D(xn) is the number of deaths in an open age group for any fixed year y. Here x1 is the lowest age used for fitting the model and xn is the lower age limit of the open age interval. The observed cumulative proportion of deaths above age xi is given by
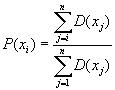 |
(3.1)
|
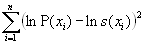 |
(3.2)
|
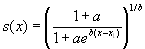 |
(3.3)
|
Given a, b, deaths by Lexis triangles in open age group are computed as follows
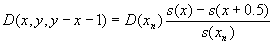 |
(3.4)
|
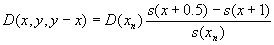 |
(3.5)
|
Generally, population estimates at higher ages are less reliable than death
registration data. The data in the K-T database pertain to very high ages where
international migration is negligible, so we can employ extinct generation method
to produce population estimates from the data on death. Figure 4.1 shows the
most common situation. Suppose that we know the number of deaths for each Lexis
triangle and that we know the highest age w
with non-zero survivor counts in the year y: ![]() for any
for any ![]() and
and
![]() for
for ![]() .
Hence cohorts attaining any age above w at
the beginning of the calendar year y are extinct, population for these
cohorts can be estimated from death counts simply by summing up deaths
starting from the highest age at death. This is essentially an extinct generation
method pioneered by Vincent in 1951.
.
Hence cohorts attaining any age above w at
the beginning of the calendar year y are extinct, population for these
cohorts can be estimated from death counts simply by summing up deaths
starting from the highest age at death. This is essentially an extinct generation
method pioneered by Vincent in 1951.
In mathematical terms, population at the beginning of year y, at age x and in cohort y-x-1 is given as (in practice summation is carried out only up to the year y - over all ages with available data)
|
|
(4.1a)
|
The population at the exact age x in the previous year and in the same cohort is
|
|
(4.1b)
|
In Fig. 4.1 extinct cohorts are represented by a bold line.
Figure 4.1 Estimating Survivors at High Ages from Data on Deaths
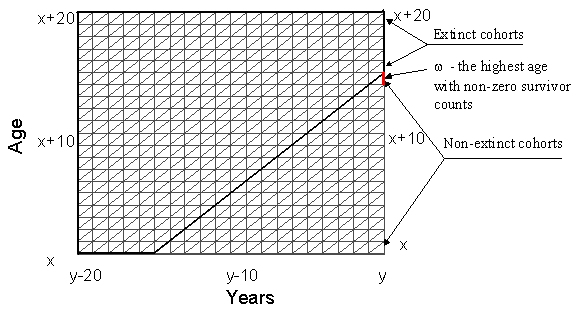
Younger cohorts, which attained age w or
lower at the beginning of the year y, are not extinct. For estimating the
population at risk in any year ![]() and
at any age
and
at any age ![]() ,
we need not only to sum up deaths above age
,
we need not only to sum up deaths above age ![]() in a particular cohort but also add the number of survivors in this cohort
at the beginning of year y:
in a particular cohort but also add the number of survivors in this cohort
at the beginning of year y:
|
(4.2)
|
In countries with reliable population registers, e.g. Sweden or Denmark, population (or survivor) estimates at the beginning of the year y are readily available from the official statistics and they can be directly added to the database. Unfortunately, this is usually not the case for other countries. Population estimates might be not available from the official statistics, i.e. given by age group 90+ only, or they could be of such bad quality that they couldn't be added to the database. We then need to estimate the number of survivors at the beginning of the year y from the number of deaths in the previous years. There are a number of such methods available. Currently, we employ the survivor ratio method adjusted to the official population above age 90 (Hereafter the latter-term refers to population estimates produced by the national statistical office).
Consider, for example, a situation where official population estimates at the beginning of the year y are given by a single age between ages 80 and 89 but at higher ages they are aggregated in a single age group 90+. Then we need to estimate the population by single year of age for ages 90, 91, etc. If we accept the official numbers both for ages 80-89 and 90+, we can employ the survivor ratio method to perform this task. Then we can incorporate survivor estimates in the database and apply the extinct cohort method for producing population estimates for the entire database (Equation 4.2).
Every non-extinct cohort attaining age ![]() at the beginning of the year
at the beginning of the year ![]() has a "survivor ratio"; i.e. the ratio of current survivors to
the death counts in the last
has a "survivor ratio"; i.e. the ratio of current survivors to
the death counts in the last ![]() calendar years:
calendar years:
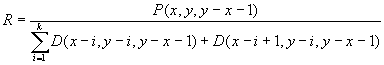
The number of deaths is known, so the idea is that if we can make estimation ![]() from past experience for each of the non-extinct cohorts, we can use
it to estimate the number of survivors.
from past experience for each of the non-extinct cohorts, we can use
it to estimate the number of survivors.
In its original form, this method is based implicitly on the assumption that
the ‘survivor ratios’ or, equally, the ![]() -ages
survival:
-ages
survival:
|
|
(5.1)
|
in two or more subsequent cohorts are the same.
Suppose that we have to estimate survivors ![]() at age
at age ![]() and in the year
and in the year ![]() .
Using the equation for
.
Using the equation for ![]() -ages
survival yields
-ages
survival yields
|
|
(5.2)
|
Here the unobserved survival ![]() in the current cohort is replaced by the average survival from age
in the current cohort is replaced by the average survival from age ![]() to
to ![]() observed
in
observed
in ![]() preceding
cohorts
preceding
cohorts
|
(5.3)
|
and the number of survivors is computed as
|
(5.4)
|
In order to start our estimates, we need to select the highest
age ![]() with
non-zero survivor counts. In general, w depends
on the calendar year, so hereafter I refer to the current year only. An estimation
of w is performed by using the average number of deaths
in preceding years (below). As soon as w is
found and the number of survivors is determined from the average number of deaths,
we incorporate the number of survivors in the database at age w
and fill all ages above w with zero survivors.
Finally, the extinct cohort population is computed for all cohorts with the known number
of survivors and computations proceed as specified above.
with
non-zero survivor counts. In general, w depends
on the calendar year, so hereafter I refer to the current year only. An estimation
of w is performed by using the average number of deaths
in preceding years (below). As soon as w is
found and the number of survivors is determined from the average number of deaths,
we incorporate the number of survivors in the database at age w
and fill all ages above w with zero survivors.
Finally, the extinct cohort population is computed for all cohorts with the known number
of survivors and computations proceed as specified above.
To find w, we select arbitrarily a very high age and compute the average number of deaths above this age in l preceding years. This arbitrary age is selected to guarantee that the total number of deaths in l preceding years above it is zero. Thus, two natural candidates are the highest age covered by the database and the highest age at death in the l preceding years. Equation 5.5 shows how the average number of deaths is computed:
|
(5.5)
|
If ![]() , then
we assign the current age to w and set all
survivors above it to zero. If
, then
we assign the current age to w and set all
survivors above it to zero. If ![]() ,
we step down to the lower age and repeat the procedure until w
is determined. Finally, we apply the extinct cohort method for all cohorts attaining
age
,
we step down to the lower age and repeat the procedure until w
is determined. Finally, we apply the extinct cohort method for all cohorts attaining
age ![]() at
the beginning of year y.
at
the beginning of year y.
At this stage we are able to apply the SR method to obtain survivor estimates
for ages below ![]() .
Once the survivor estimate for the age
.
Once the survivor estimate for the age ![]() is computed, we apply the extinct cohort method to compute population estimates
for the whole cohort attaining age
is computed, we apply the extinct cohort method to compute population estimates
for the whole cohort attaining age ![]() at the beginning of year y. Then we repeat this procedure for age
at the beginning of year y. Then we repeat this procedure for age
![]() and so
on.
and so
on.
In the method described so far, we did not make any assumptions about trends in death rates over time, assuming that mortality is constant. It turns out that the population estimates produced by this procedure are increasingly lower than the actual numbers of survivors as we proceed to the lower ages. This is mostly due to the mortality decline at older ages in the contemporary populations [Kannisto, 1994]. To account for this decline in mortality, the SR can be extended by introducing an additional parameter c:
|
|
(5.6)
|
This relaxes the assumption underlying Equations 5.3
and 5.4. The constant ![]() is interpreted as a ratio of the odds of survival in the current cohort to the
odds in the preceding
is interpreted as a ratio of the odds of survival in the current cohort to the
odds in the preceding ![]() cohorts. If death rates are declining over time, this constant will be higher
than one, and by selecting an appropriate value of
cohorts. If death rates are declining over time, this constant will be higher
than one, and by selecting an appropriate value of ![]() ,
we can make a correction to the mortality decline that is not captured by
Equation 5.4.
,
we can make a correction to the mortality decline that is not captured by
Equation 5.4.
The idea of correcting the mortality decline inevitably raises the question of how to chose c in an objective manner? A reasonable approach would be to select c in such way that our population estimates will be coherent with the official population estimates. Usually, the national statistical office provides population estimates for ages above 90. So we can take advantage of this information and choose c in a way that our population estimates for ages above 90 will be the same as the official ones. The constant c is not an arbitrary chosen parameter rather it is estimated internally in the method to meet constraint imposed by the official population. The choice of correction coefficient c has been tested on reliable data from nine countries and compared with other possible methods for choosing c and other survivor estimates methods (a description of other survivor estimate methods can be found in [Andreev, 1999].). The results indicate that this assumption is a good practical choice.
To summarize, the survivor ratios method SR(k, m, Px+) depends
on three parameters: k , i.e. the number of ages used for the estimation of survivor
ratios; m, the number of preceding cohorts; and Px+,
an official population estimates for ages above x used to select the
correction coefficient c in such way that the estimated population ![]() .
.
Finally, I would like to describe the algorithm based on the SR method, which is used currently for producing survivor estimates:
The range of ages for which we can accept the official counts and for which we use the SR estimates depends on the results of the data checks and data availability. Whenever possible, we are trying to use the SR estimates for ages above 90 and incorporate official population numbers for lower ages. Even if the official population is available for ages 90, 91, 92, 93, 94, 95+, for the sake of uniformity we still use the survivor estimates produced by the SR method for ages above 90.
6. Computations of period life tables by cohort method
This section describes method of the computations of period life tables for the period y1 to y2.
Nx denotes the population at the exact age x over the period y1 to y2.
|
|
(6.1)
|
Note that the population in the year y2 is not
included in Nx, i.e. is the number of years used for the computation
of Nx is ![]() .
Throughout this text and in the output life table files, we specify the period covered
by life table as from y1 to y2. Table 6.1
shows period life table for the population of England and Wales computed for years
1990-1998. The population at risk at age 80 N80=821355
given in Table 6.1 is computed by summing up the column POPULATION for
the following Lexis triangles from the Lexis database incorporating data for
England and Wales, males:
.
Throughout this text and in the output life table files, we specify the period covered
by life table as from y1 to y2. Table 6.1
shows period life table for the population of England and Wales computed for years
1990-1998. The population at risk at age 80 N80=821355
given in Table 6.1 is computed by summing up the column POPULATION for
the following Lexis triangles from the Lexis database incorporating data for
England and Wales, males:
|
YEAR |
AGE |
TRIANGLE |
COHORT |
POPULATION |
DEATHS |
|
1990 |
80 |
1 |
1910 |
102161 |
5017 |
|
1991 |
80 |
1 |
1911 |
103242 |
4940 |
|
1992 |
80 |
1 |
1912 |
105619 |
4938 |
|
1993 |
80 |
1 |
1913 |
107478 |
5146 |
|
1994 |
80 |
1 |
1914 |
107668 |
4990 |
|
1995 |
80 |
1 |
1915 |
105212 |
4967 |
|
1996 |
80 |
1 |
1916 |
99257 |
4668 |
|
1997 |
80 |
1 |
1917 |
90718 |
4168 |
|
821355 |
This column includes deaths counts occurred in the population reached the exact
age x during period ![]() over one year of age:
over one year of age:
![]() (6.2)
(6.2)
For example, D80=76373 given in Table 6.1 is computed by summing up death counts in the following records of the Lexis database:
|
YEAR |
AGE |
TRIANGLE |
COHORT |
POPULATION |
DEATHS |
|
1990 |
80 |
1 |
1910 |
102161 |
5017 |
|
1991 |
80 |
2 |
1910 |
97144 |
4940 |
|
1991 |
80 |
1 |
1911 |
103242 |
4940 |
|
1992 |
80 |
2 |
1911 |
98302 |
4937 |
|
1992 |
80 |
1 |
1912 |
105619 |
4938 |
|
1993 |
80 |
2 |
1912 |
100681 |
5146 |
|
1993 |
80 |
1 |
1913 |
107478 |
5146 |
|
1994 |
80 |
2 |
1913 |
102332 |
4990 |
|
1994 |
80 |
1 |
1914 |
107668 |
4990 |
|
1995 |
80 |
2 |
1914 |
102678 |
4967 |
|
1996 |
80 |
2 |
1915 |
100245 |
4668 |
|
1995 |
80 |
1 |
1915 |
105212 |
4967 |
|
1996 |
80 |
1 |
1916 |
99257 |
4668 |
|
1997 |
80 |
2 |
1916 |
94589 |
4168 |
|
1997 |
80 |
1 |
1917 |
90718 |
4168 |
|
1998 |
80 |
2 |
1917 |
86550 |
3723 |
|
76373 |
This columns contains the age specific probability of dying
|
|
(6.3)
|
This column includes the survival function
|
|
(6.4)
|
with ![]() at
the first age of the life table equals 100000. The highest age appeared in the
life table is determined by qx column. The calculations are
stopped at the lowest age with qx = 1 or qx
= . (missing value) with survival at the next age assigned to zero and lx+1=0.
at
the first age of the life table equals 100000. The highest age appeared in the
life table is determined by qx column. The calculations are
stopped at the lowest age with qx = 1 or qx
= . (missing value) with survival at the next age assigned to zero and lx+1=0.
The dx denotes the death density function:
|
|
(6.5)
|
Lx denotes the total time lived by the whole population between the exact ages x and x+1:
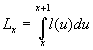
The computation of this column is based on the usual assumption of a linear change of survival function between age x and x+1:
|
|
(6.6)
|
Tx denotes the total time lived by the whole population after age x:
|
|
(6.7)
|
or
![]()
This column includes the remaining life expectancy at age x:
|
|
(6.8)
|
Table 6.1 Period life table for England and Wales, Males, years 1990-1998.
|
Age |
Nx |
Dx |
qx |
lx |
dx |
Lx |
Tx |
ex |
|
80 |
821355 |
76373 |
0.0930 |
100000 |
9298 |
95351 |
658060 |
6.58 |
|
81 |
753305 |
75487 |
0.1002 |
90702 |
9089 |
86157 |
562709 |
6.20 |
|
82 |
676220 |
74185 |
0.1097 |
81613 |
8953 |
77136 |
476552 |
5.84 |
|
83 |
594160 |
70860 |
0.1193 |
72659 |
8665 |
68327 |
399416 |
5.50 |
|
84 |
511861 |
66351 |
0.1296 |
63994 |
8295 |
59846 |
331090 |
5.17 |
|
85 |
433142 |
60508 |
0.1397 |
55699 |
7781 |
51808 |
271243 |
4.87 |
|
86 |
361152 |
54350 |
0.1505 |
47918 |
7211 |
44312 |
219435 |
4.58 |
|
87 |
296127 |
48302 |
0.1631 |
40707 |
6640 |
37387 |
175123 |
4.30 |
|
88 |
237481 |
41436 |
0.1745 |
34067 |
5944 |
31095 |
137737 |
4.04 |
|
89 |
186731 |
35097 |
0.1880 |
28123 |
5286 |
25480 |
106642 |
3.79 |
|
90 |
143005 |
28973 |
0.2026 |
22837 |
4627 |
20524 |
81162 |
3.55 |
|
91 |
105972 |
22733 |
0.2145 |
18210 |
3906 |
16257 |
60638 |
3.33 |
|
92 |
76862 |
18245 |
0.2374 |
14304 |
3395 |
12606 |
44382 |
3.10 |
|
93 |
53924 |
13771 |
0.2554 |
10908 |
2786 |
9516 |
31775 |
2.91 |
|
94 |
36808 |
9996 |
0.2716 |
8123 |
2206 |
7020 |
22260 |
2.74 |
|
95 |
24587 |
7182 |
0.2921 |
5917 |
1728 |
5053 |
15240 |
2.58 |
|
96 |
15990 |
4960 |
0.3102 |
4188 |
1299 |
3539 |
10188 |
2.43 |
|
97 |
10167 |
3403 |
0.3347 |
2889 |
967 |
2406 |
6649 |
2.30 |
|
98 |
6247 |
2077 |
0.3325 |
1922 |
639 |
1603 |
4243 |
2.21 |
|
99 |
3894 |
1436 |
0.3688 |
1283 |
473 |
1047 |
2640 |
2.06 |
|
100 |
2313 |
865 |
0.3740 |
810 |
303 |
658 |
1594 |
1.97 |
|
101 |
1365 |
547 |
0.4007 |
507 |
203 |
405 |
936 |
1.85 |
|
102 |
783 |
343 |
0.4381 |
304 |
133 |
237 |
530 |
1.74 |
|
103 |
414 |
182 |
0.4396 |
171 |
75 |
133 |
293 |
1.71 |
|
104 |
216 |
100 |
0.4630 |
96 |
44 |
74 |
160 |
1.67 |
|
105 |
112 |
44 |
0.3929 |
51 |
20 |
41 |
86 |
1.67 |
|
106 |
65 |
28 |
0.4308 |
31 |
13 |
24 |
45 |
1.43 |
|
107 |
36 |
19 |
0.5278 |
18 |
9 |
13 |
20 |
1.14 |
|
108 |
14 |
9 |
0.6429 |
8 |
5 |
6 |
7 |
0.86 |
|
109 |
5 |
5 |
1.0000 |
3 |
3 |
1 |
1 |
0.50 |
|
110 |
0 |
6.9 Life tables for countries with data available for ages 80-99 only
If death counts for a certain country are not available above age 100, we are not able to compute death rates by single year of age above 100. In this case the period life tables will be calculated only up to age 99, leaving life expectancy e100 unknown. In order to fill ex, Lx and Tx columns, Kannisto suggested the following estimator of e100:
|
|
(6.9)
|
Having computed e100, we are able to complete computations of all three columns in the conventional way.
6.10 Period life tables for an aggregate of countries
6.10.1 Life table for aggregated population
Period life tables for an aggregated population are produced in the same way from total population Nx and deaths Dx in all countries included in the aggregate:
![]()
and
![]()
where ![]() and
and
![]() denote
the population at risk and the corresponding death numbers for country i
included in the aggregated population.
denote
the population at risk and the corresponding death numbers for country i
included in the aggregated population.
6.10.2 Life table based on averaging country-specific probabilities of death
Here, the life table has to be computed from the average of the country-specific probabilities of death:
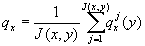
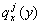 is the probability of death at age x in calendar year y from the country
j. Then lx, dx, Lx,
Tx, ex are calculated according to the formulae (6.4), (6.5), (6.6), (6.7), (6.8).
is the probability of death at age x in calendar year y from the country
j. Then lx, dx, Lx,
Tx, ex are calculated according to the formulae (6.4), (6.5), (6.6), (6.7), (6.8).
See also handling missing values and computation of indicators.
6.11 Handling missing values in life table computations
Problems with missing values arise virtually in any computations based on data from the K-T database. For example, consider a computation of an aggregated life table for the years 1985-1994. Suppose also that for most countries data are available for the whole range of years but for a few of them for shorter periods only. We then need to decide how to compute the aggregated population and deaths for the last year. Should we use only data from the countries with available data or do we need to shorten the period covered by the life table? What should we do if in some country the data are missing at some ages or cohorts?
In this case, missing values can be handled in different ways. For example, we can require that the data for all countries and for all ages must be available for computing an aggregated life table. Alternatively, we can require that the data for at least one country must be available at a certain age and year in order to compute the whole life table. Of course, various intermediate variations are possible as well.
Currently, we are using the second approach. Suppose that we need to compute an aggregated life table for the period y1 to y2. The aggregated population at risk and the number of corresponding deaths over one year of age are
|
|
(6.10)
|
where ![]() and
and ![]() denotes
the population at risk and the corresponding number of deaths for i country
included in the aggregated life table.
denotes
the population at risk and the corresponding number of deaths for i country
included in the aggregated life table.
For i country:
|
|
(6.11a)
|
|
|
(6.11b)
|
An elementary element of the Lexis diagram in this case is a horizontal
parallelogram with the population at risk ![]() and the corresponding number of deaths is
and the corresponding number of deaths is ![]() .
If at least one of these three quantities is missing, we consider the data
missing for the whole Lexis parallelogram. In this case, its data
are excluded from the computations. Thus, the quantities
.
If at least one of these three quantities is missing, we consider the data
missing for the whole Lexis parallelogram. In this case, its data
are excluded from the computations. Thus, the quantities![]() and
and![]() are aggregated numbers of the population and deaths for ith country
with possible removal of the Lexis parallelograms with missing values. A missing
value is assigned to
are aggregated numbers of the population and deaths for ith country
with possible removal of the Lexis parallelograms with missing values. A missing
value is assigned to ![]() and
and ![]() if all
data in the i country for the period
if all
data in the i country for the period ![]() are missing. Similarly, a missing value is assigned to Nx
and Dx if all data for all countries are missing.
As the computation of Nx and Dx columns is completed,
other columns of the life table are calculated in a standard way.
are missing. Similarly, a missing value is assigned to Nx
and Dx if all data for all countries are missing.
As the computation of Nx and Dx columns is completed,
other columns of the life table are calculated in a standard way.
6.12 Computation of indicators
6.12.1 Population for the range of ages Nx1, x2(y) for year y
Calculation can be performed for an aggregated population or/and for country-populations:
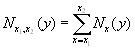
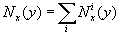
where ![]() denotes
the population at risk for i country included in the aggregated population.
denotes
the population at risk for i country included in the aggregated population.
6.12.2 Deaths at ages for the range of ages Dx1, x2(y) for year y
Calculations can be performed for the aggregated population or/and for country-populations:
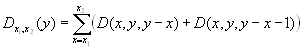
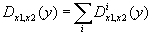
where i denotes country i in the aggregated population.
6.12.3 Median age of population
Calculation can be performed for the aggregated population or/and for country-populations. First, the total population size is obtained by summing up the age-specific counts:
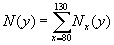
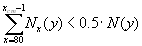
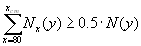
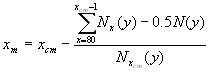
6.12.4 Median length of life
The calculation can be performed from the aggregated life table or/and for country-specific life tables with radix l80=100000. By sequential testing x=80, 81,.... we find the crude median age xcm, for which:
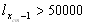
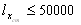
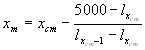
6.12.5 Average life expectancy for the range of ages
The calculation can be performed from an aggregated life table or/and for country-specific life tables. The following formula is used:
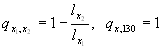
6.12.6 Probability of death age ranges
The following formula is used:
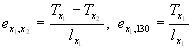
This problem arises if we need population estimates for January 1st in a given year but census population is available only for the previous year (not necessarily refering to the beginning of this year). For example, in Japan the reference day of the 1995 census was October 1st, and to obtain the population estimates for January 1st 1996 we need to adjust the census population by deaths and migration in the last months of the year 1995.
As regards the K-T database, the method described in this section is used for producing population estimates for the last year if official population estimates for this year do not exist. The procedure is based on the following assumptions:
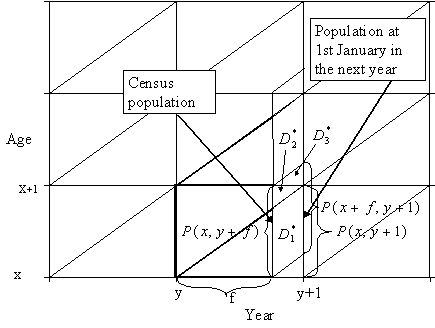
Figure 7.1 illustrates obtaining population estimates in the year y+1.
Figure 7.1. Computing population estimates at the beginning of a certain year from population and deaths in the previous year.
Let![]() be population
estimates at age x (most likely it is the census population but not necessarily
limited to it) in the year y+f. The f (
be population
estimates at age x (most likely it is the census population but not necessarily
limited to it) in the year y+f. The f (![]() )
denotes the fraction of the year, for example f=273/365 for October, 1st.
Let
)
denotes the fraction of the year, for example f=273/365 for October, 1st.
Let ![]() be deaths
occurred in this population until the next year. These deaths occur in three
different Lexis triangles and we use index i to enumerate them (see Figure
7.1). If deaths are distributed evenly over a Lexis triangle, we arrive at:
be deaths
occurred in this population until the next year. These deaths occur in three
different Lexis triangles and we use index i to enumerate them (see Figure
7.1). If deaths are distributed evenly over a Lexis triangle, we arrive at:
|
|
(7.1a)
|
|
|
(7.1b)
|
|
|
(7.1c)
|
and the population aged x+f at January 1st in the year y+1 will be
|
|
(7.2)
|
This population cannot be directly incorporated in the database because it is f year older than required. By using linear interpolation
|
|
(7.3)
|
we can compute population estimates at 1st January as required by the database.
This method is easily generalized if census population estimates are available far back in the past. In this case we promote the census population to the January 1st of the next year and then subtract deaths from the promoted population (deaths by single year, age and cohort are assumed to be available until the last year).
The Lexis files are provided in text format. We use a CRLF ("\r\n") combination of characters as a record delimiter and a comma "," as a field delimiter. Field names are given in the first line of each file. All data are integers. Missing values are coded as a single point ".". Optionally, the data files can contain a number of spaces to improve text file readability. The spaces included in the text files do not have any other function.
This example shows a few lines for a Lexis database:
Year, Age, Triangle, Cohort, Population, Deaths
1911, 80, 1, 1831, 17026, 1203
1911, 80, 2, 1830, ., .
1911, 81, 1, 1830, 14886, 1057
Note the missing values for POPULATION and DEATHS in the third column.
8.2 Format of the period life tables
Similar to the text format of the Lexis database, we are using CRLF characters as a record delimiter and a comma as a field delimiter. In addition to the life table columns specified in Section 6, two other columns indicating the period covered by the life table are included (e.g. Table 6.1):
FirstYear, LastYear, Age,Nx,Dx,qx,lx,dx,Lx,Tx,ex
1990,1998,80,821355,76373,0.0930,100000,9298,95351,658060,6.58
1990,1998,81,753305,75487,0.1002,90702,9089,86157,562709,6.20
1990,1998,82,676220,74185,0.1097,81613,8953,77136,476552,5.84
1990,1998,83,594160,70860,0.1193,72659,8665,68327,399416,5.50
1990,1998,84,511861,66351,0.1296,63994,8295,59846,331090,5.17
Life table files are sorted by the columns "FirstYear", "LastYear" and "Age". Columns "FirstYear", "LastYear", "Age", "Nx", "Dx", lx dx Lx Tx columns are given as integers; column "qx" is provided in the fixed-point format with four decimal places and column "ex" with two decimal places.
Precision of output number specified according to recommendations by V. Kannisto.
[ Return to last page | Return to Home Page ]
© 2004 Max-Planck-Gesellschaft