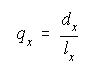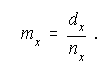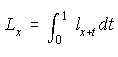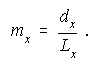For a given cohort or other group of individuals, we denote by ![]() the number who
survive to reach the exact age x. (This is the traditional notation: the letter
"l" originally stood for "lives". In life tables,
the number who
survive to reach the exact age x. (This is the traditional notation: the letter
"l" originally stood for "lives". In life tables, ![]() is often taken as
100,000). Out of these
is often taken as
100,000). Out of these![]() individuals, the number who survive for 12 months, and so reach the exact age
individuals, the number who survive for 12 months, and so reach the exact age
![]() , is
, is ![]() . The number who died
within the 12 months is therefore
. The number who died
within the 12 months is therefore
|
(1) |
and the proportion who died is
|
(2) |
If the numbers are sufficiently large, ![]() gives an estimate of
the probability of dying within 12 months of reaching age x.
gives an estimate of
the probability of dying within 12 months of reaching age x.
Alternatively, if a theoretical model provides an estimate that the probability of dying
is ![]() , and if we
know that the number who reached age x was
, and if we
know that the number who reached age x was ![]() , then we can estimate that the number of deaths
will be
, then we can estimate that the number of deaths
will be ![]() . In
the literature,
. In
the literature, ![]() is often described as the rate of mortality, or (in France) as the quotient of mortality.
is often described as the rate of mortality, or (in France) as the quotient of mortality.
Definition of ![]() , the central death rate
, the central death rate
For a given population or cohort, the central death rate at age x
during a given period of 12 months is found by dividing the number of people who died
during this period while aged x (that is, after they had reached the exact age x
but before reached the exact age ![]() ) by the average number who were living in that age group
during the period.
) by the average number who were living in that age group
during the period.
The simplest case is for a
stationary population, in which the number of people who leave the age group during the
year (either by reaching age ![]() or by dying) is exactly balanced by the number who enter the age
group on reaching their x-th birthday. In this simple case, the number living in the age
group is constant throughout the year, say
or by dying) is exactly balanced by the number who enter the age
group on reaching their x-th birthday. In this simple case, the number living in the age
group is constant throughout the year, say ![]() . If the number of deaths at age x is
. If the number of deaths at age x is ![]() , then the central
death rate
, then the central
death rate ![]() is
given by
is
given by
|
(3) |
For an observed population which is not
stationary, ![]() can still be measured and
can still be measured and ![]() can often be estimated as the average of the observed
populations aged x at the beginning and end of the 12 months, or as the
population at mid-year.
can often be estimated as the average of the observed
populations aged x at the beginning and end of the 12 months, or as the
population at mid-year.
However, for cohorts with a known survival function ![]() we can do better than this. The average number
living at age x during the year is
we can do better than this. The average number
living at age x during the year is
|
(4) |
and the central death rate is given by
|
(5) |
See Pollard (1973).
Definition of ![]() , the force of mortality
, the force of mortality
The central death rate ![]() is defined by (3) and (5) as the deaths in 12
months divided by the average population over 12 months. It is a measure of deaths per
head of population per unit time, where in this case the unit of time is 12 months. We
could repeat this calculation taking the period as 6 months instead of 12 months (but
converting the result to an annual rate), and then over shorter and shorter periods, until
we finally reach the instantaneous death rate
is defined by (3) and (5) as the deaths in 12
months divided by the average population over 12 months. It is a measure of deaths per
head of population per unit time, where in this case the unit of time is 12 months. We
could repeat this calculation taking the period as 6 months instead of 12 months (but
converting the result to an annual rate), and then over shorter and shorter periods, until
we finally reach the instantaneous death rate ![]() . This is also known as the hazard rate.
. This is also known as the hazard rate.
In
the notation of the calculus, the number of deaths between ages x and ![]() ,
in a cohort with the survival function
,
in a cohort with the survival function ![]() , is
, is ![]() The instantaneous death rate (i.e. deaths per head of population per unit
time) is
The instantaneous death rate (i.e. deaths per head of population per unit
time) is
|
(6) |
With ![]() defined in this way, the probability of dying
between age x and age
defined in this way, the probability of dying
between age x and age ![]() is
is ![]() .
.
We
note that ![]() is a
continuous function, which gives it certain advantages. For example, it can be used to
calculate the probability of dying within periods of any length, not just multiples of 12
months.
is a
continuous function, which gives it certain advantages. For example, it can be used to
calculate the probability of dying within periods of any length, not just multiples of 12
months.
Although ![]() can
never exceed 1, both
can
never exceed 1, both ![]() and
and ![]() can do so. Consider, for example, a cohort in which 8 members reach age x,
of whom 7 die within 12 months.
can do so. Consider, for example, a cohort in which 8 members reach age x,
of whom 7 die within 12 months.
The relationship between ![]() and
and ![]()
In a cohort, the central death rate ![]() relates to all deaths between the exact age x
and the exact age
relates to all deaths between the exact age x
and the exact age ![]() . The force of mortality, being a continuous function, gives the instantaneous
death rate at each separate age within this interval. More specifically,
. The force of mortality, being a continuous function, gives the instantaneous
death rate at each separate age within this interval. More specifically, ![]() gives the
instantaneous death rate at every age
gives the
instantaneous death rate at every age ![]() , where
, where ![]() . From one point of view,
. From one point of view, ![]() can be regarded as a kind of average of all the
instantaneous death rates in this interval.
can be regarded as a kind of average of all the
instantaneous death rates in this interval.
It is
therefore not surprising to find that ![]() is generally quite close to the instantaneous death rate (i.e.,
the force of mortality) in the middle of that interval. That is to say, there is an
approximate relationship
is generally quite close to the instantaneous death rate (i.e.,
the force of mortality) in the middle of that interval. That is to say, there is an
approximate relationship
|
(7) |
where the symbol ![]() means "approximately equals". This
approximation is given by Pollard (1973), who gives a more formal derivation.
means "approximately equals". This
approximation is given by Pollard (1973), who gives a more formal derivation.
It is
of interest to see the maximum possible error in the approximation (7) in two extreme
cases. If![]() increases exponentially with age, as in the Gompertz model
increases exponentially with age, as in the Gompertz model ![]() then when
then when ![]() and
and ![]() it can be shown that
the error in (7) is at the most 0.8 per cent. On the other hand, when
it can be shown that
the error in (7) is at the most 0.8 per cent. On the other hand, when ![]() is constant, the
error in (7) is zero. All the models considered in this Monograph fall between these two
extremes.
is constant, the
error in (7) is zero. All the models considered in this Monograph fall between these two
extremes.
The relationship between ![]() and
and ![]()
From the definitions (1) and (2), it follows that
|
(8) |
There is also a well-known exact equation, which can be proved by integrating (6), which states that
|
(9) |
If we combine (8) with (9), and assume that the integral
of ![]() between x
and
between x
and ![]() will be
close to the value
will be
close to the value ![]() at the mid-point of this interval, we obtain the approximations
at the mid-point of this interval, we obtain the approximations
|
(10) |
|
(11) |
The accuracy of these approximations can be
examined in the same way as before, by considering extreme cases. When ![]() increases
exponentially with age, as in the Gompertz model
increases
exponentially with age, as in the Gompertz model ![]() then when
then when ![]() the error in (10) is only 0.04 per cent,
irrespectively of the value of
the error in (10) is only 0.04 per cent,
irrespectively of the value of ![]() . When
. When ![]() is constant, both (10) and (11) hold exactly. Thus both these
approximations are highly accurate, in all the models considered in this Monograph.
is constant, both (10) and (11) hold exactly. Thus both these
approximations are highly accurate, in all the models considered in this Monograph.
Other approximations
By combining (7) with (10) and (11) we obtain
|
(12) |
|
(13) |
By similar methods, it is also possible to derive
|
(14) |
where ![]()
By a
judicious choice and use of the approximations (7) and (10)-(14), it is possible to
convert between ![]() ,
,
![]() and
and ![]() at will.
at will.