Beijing Presentation

XXIII^rd IUSSP General Population Conference
Beijing, China
Second Plenary Session
17 October 1997

I am a demographer. Like all good demographers, I like China. China is where the people are, the most populous nation on earth. China is also the home of many excellent demographers, many of them here today. Chinese demographers have made outstanding contributions to deepening knowledge of the structure and dynamics of the population of China. They have also made substantial contributions to the development of demographic models and methods, of interest and of use around the world. My closest friend among Chinese demographers is Prof. Zeng Yi from Peking University; many of the insights and findings about population aging that I will discuss today are drawn from my collaboration with him. Other research findings stem from collaboration with Dr. Zhao Zhongwei, Mrs. Wang Zhenglian, and Mr. Tan Qihua. My first trip to China was a decade ago and this is my fifth visit. I hope to enjoy many productive visits in the future.

As the IUSSP meeting draws to a close, we can all express our deep appreciation to the organizers and to our Chinese hosts. This has been a very fruitful, highly successful meeting, full of life and full of ideas. I am very pleased that I was able to attend the meeting and benefit from it. And I am very grateful that I was given the opportunity to talk with you today about the demography of aging.

Before getting into that topic, however, I would like to share with you my view of the nature of the field of demography. What is demography? It seems to me that demography rests on the solid foundations of mathematics and statistics. We demographers like numbers, especially censuses and official statistics, and we like calculations and formulas. We like to count and it is our ability to count that gives us insights and influence. We have influence because demography is of great interest to the public and of considerable importance to policymakers. So demography rests on the bedrock of mathematics and statistics but its research findings float upward into the windy heights of politics and policymaking.

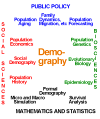
The models and methods of demography shed light on the structure and dynamics of populations. Most of us are mainly interested in human populations, but Alfred Lotka, Raymond Pearl, and many other distinguished demographers have also had a deep interest in animal populations. Furthermore, the two things we study most—namely fertility and mortality—are quite biological. Hence, as shown in Figure 1, I see demography as lying at the meeting ground between the social sciences on the one hand, including sociology, economics, geography, history, and cultural anthropology, and the biological sciences on the other hand, including epidemiology, ecology, genetics, and biological anthropology.

Figure 1: The Location of Demography in the World of Knowledge.
(Click on figure for full view)

My talk today will blend mathematics and statistics with policy analysis and insights from the biological sciences with insights from the social sciences.

The populations of most of the world's countries are growing older. This shift is creating a new demography, a demography of low fertility and long lives. The rapidly growing populations of the elderly are putting unprecedented stresses on societies, because new systems of financial support, social support, and health care have to be developed and implemented. A century ago most of the people born around the world died before they had children; most of the people who had children died before their children had children. Elderly people were unusual and extended, three-generation families represented only a small fraction of all families. Today, in many countries including China, the typical newborn can expect to survive to see the birth not only of children and grandchildren but great-grandchildren as well.

I will touch briefly today on some of the health, social, and economic issues arising from the rapid growth in the numbers of older people and the shift of the age-distribution of populations to older ages. I cannot even start, however, to do justice to all the interesting research demographers have done on the problems and opportunities associated with population aging. So I would like to focus my talk on a particular research thrust, namely demographic analyses of survival and longevity. I will review research done by many researchers, some in Germany at the new Max Planck Institute for Demographic Research in Rostock, some in Denmark at the new Danish Center for Demographic Research in Odense, some in England, France, Italy, Sweden, Finland, and elsewhere in Europe, some in the United States, some in Mexico, and some in China.

Let me start with a review of the remarkable improvements in survival at older ages in recent decades.

“There is one and only one cause of death at older ages. And that is old age. And nothing can be done about old age.” This verbal pronouncement by Leonard Hayflick, a pioneering gerontologist, captures the gist of a prevalent syndrome of beliefs. Because deaths at younger ages are now unusual in developed countries, this view implies that human life expectancy—in the developed countries and in China and many other developing countries with low mortality—is close to the limit imposed by biology. The population of older people will grow as the baby boom ages but if this view is correct governments need not worry that enhanced survival at older ages might accelerate the growth. Furthermore, the view that mortality at older ages is intractable leads to the conclusion that health-care resources and biomedical research should increasingly be directed toward improving “the average well-being of the population” rather than extending “the average lifespan” (Lohman, Sankarana-rayanan, and Ashby 1992; see Olshansky, Carnes, and Cassel 1990 for a subtler conclusion).

Mortality at older ages is, however, by no means intractable (Wilmoth 1997). In fact, remarkable progress has been made since 1950 and especially since 1970 in substantially improving survival at older ages, even the most advanced ages. Despite this compelling evidence, the belief that old-age mortality is intractable remains deeply held by many people. Because of its implications for social, health, and research policy, the belief is pernicious. Because the belief is so prevalent, forecasts of the growth of the elderly population are too low, expenditures on life-saving health-care for the elderly are too low, and expenditures for biomedical research on the deadly illnesses of old age are too low.

The fact is that mortality at older ages has fallen dramatically since 1950 in developed countries and most developing countries as well. Figure 2 shows the progress that has been made in Sweden for females aged 85, 90, and 95. Most older people are female, so for simplicity only female data are presented in most of the tables and figures of this review. Similar patterns to those shown in Figure 2 exist in most other developed countries and many developing countries. Similar patterns also hold for males, although male gains have generally been smaller than female gains (Kannisto 1994, 1996; Kannisto et al. 1994)). The curves are jagged because population sizes at these ages are small and because of the impact of infectious-disease epidemics and other irregular factors. Before 1950 or so, mortality improvements at older ages were slow, but after 1950 and especially after 1970 the improvements are impressive.

Figure 2: Improvements in Mortality from 1900 through 1992 in Sweden for Females Aged 85, 90, and 95.
(Click on figure for full view)

Note: m denotes the central death rate. Source: Compiled by author from data in the Kannisto-Thatcher Oldest-Old Database, Odense University, Denmark (Kannisto 1994).

Figure 3 shows the pattern of mortality decline since 1950 for female octogenarians and nonagenarians in four representative countries: England & Wales, France, Sweden, and Japan. Note the particularly impressive performance of Japan.

Figure 3: Mortality Reductions since 1950 for Female Octogenarians and Nonagenar-ians in England & Wales, France, Sweden, and Japan.
(Click on figure for full view)

The pace of mortality improvement at older ages has been accelerating over recent decades. This is shown in Figure 4 for male and female octogenarians and nonagenarians in an aggregation of nine countries with reliable data.

Figure 4: Average Annual Improvement in Mortality Between Successive Five-Year Periods, for Male and Female Octogenarians and Nonagenarians, in an Aggregation of 10 Countries.
(Click on figure for full view)

Source: Same as Figure 2. See Kannisto et al. (1994) for method of calculation. The 10 countries are: Austria, Denmark, Finland, Germany, Iceland, Italy, Japan, Norway, Sweden, and Switzerland.

Another, longer-term perspective is provided in Table 1, which documents the acceleration of mortality improvements for females in the Nordic countries of Denmark, Finland, Norway, and Sweden, countries for which reliable mortality data at older ages are available well back into the 19th century.

Table 1: Average annual rates of improvement in female mortality (in %) for aggregation of Denmark, Finland, Norway and Sweden, for sexagenarians, septuagenarians, octogenarians, and nonagenarians, over successive 20-year periods.

Age Category
	60s	70s	80s	90s
1900s -- 1920s	0.3	0.2	0.1	0.0
1920s -- 1940s	0.7	0.4	0.2	0.0
1940s -- 1960s	1.7	1.0	0.6	0.5
1960s -- 1980s	1.5	2.1	1.7	1.2

Source: Same as Figure 2. See Kannisto et al. (1994) for description of how average annual rates of improvement are calculated.

Table 2 displays death rates by age and time for females in the Nordic countries. The increase in death rates with age is striking. The decrease in death rates over time is also striking.

Table 2: Female central death rates (in %) for aggregation of Denmark, Finland, Norway, and Sweden, for sexagenarians, septuagenarians, octogenarians, nonagenarians, and centenarians, in two periods, 1930-49 and 1989-1993.

Age Category
	60s	70s	80s	90s	100s
1930 -- 1949	2.4	6.4	16.1	33.9	70.1
1989 -- 1993	1.1	3.1	9.1	23.4	48.5
change	1.3	3.3	7.0	10.5	21.6

Source: Same as Figure 2. See Kannisto et al. (1994) for description of how average annual retes of improvement are calculated.

If mortality is reduced, then the number of lives saved is proportional to the absolute decline rather than the relative decline. For instance, if the probability of death at some age is reduced from 20% to 15%, then an extra 5% of the population continue to enjoy life. In the last row of Table 2, the absolute improvements in Nordic female mortality are displayed. It is at the most advanced ages that the most lifesaving has occurred. On second thought, this may not seem so surprising because it is at the highest ages that death rates are very high. Moreover, lives saved at the highest ages are generally not extended for more than a few years. Nonetheless, the large absolute reductions in mortality among centenarians and nonagenarians is a remarkable achievement, at sharp variance with the view that old-age mortality is intractable.

If death rates at older ages were approaching a biological limit, then it might be expected that improvements in countries with the lowest death rates would tend to be slower than in countries with death rates further away from the irreducible minimum. As illustrated in Figure 5, however, there is no correlation, either for males or for females, between levels of mortality and rates of mortality improvement. Furthermore, males suffer higher mortality than females, but rates of improvements for females are higher than for males. Figure 5 only shows a few countries, but examination of many more countries yields the same result (Kannisto et al. 1994).

Figure 5: Average Central Death Rate in the 1970s Compared with Average Annual Improvement in Mortality from the 1970s to the 1980s, for Males and Females, for Ages 80-99 Combined.
(Click on figure for full view)

Note: The subscripts f and m stand for female and male. The capital letters represent countries as follows: A, Austria; Au, Australia; Dk, Denmark; Ew, England & Wales; Sf, Finland; F, France; H, Hungary; J, Japan; and S, Sweden. Source: Same as Figure 2; also see Kannisto et al. (1994)

Much of the data used in the tables and figures so far comes from a database developed and compiled by Vaino Kannisto and Roger Thatcher (Kannisto 1994, 1996; Kannisto et al. 1994). This database includes most of the developed countries of the world, but not the United States. Until recently, demographers have been very wary of using U.S. mortality data at older ages because of concerns about the validity of age-reporting. New data sources, carefully checked by meticulous analysts, now permit accurate estimation of U.S.

Figure 6 compares some of these estimates with estimates for England & Wales and Japan. The corresponding trajectories for France and Sweden are very close to the Japanese curve. Two age-trajectories of white female mortality are shown for the United States, one for people from the Upper Midwest states of Minnesota and North and South Dakota (which is an area of exceptionally low mortality) and the other for people from the Deep South states of Arkansas, Louisiana, Mississippi, and Alabama (an area of relatively high mortality and an area in which age-misreporting might be particularly prevalent). Death rates in the Deep South remain above those in the Upper Midwest up to the late 90s: this suggests that the data may be reasonably reliable

Figure 6: Mortality in England & Wales, Japan, the United States, and Two U.S. Regions—the Upper Midwest and the Deep South—from Age 80 to 99 in 1980-1989.
(Click on figure for full view)

Note: m denotes central death rates. For the United States the figures pertain to the white population. The Upper Midwest includes Minnesota and North and South Dakota. The Deep South includes Arkansas, Louisiana, Alabama, and Mississippi. People are classified by the region in which they were living when they received their Social Security numbers. Source: For England & Wales and Sweden, same as Figure 2. For the United States and the two U.S. regions, compiled by the author from data provided by the U.S. Health Care Financing Administration.

In both regions of the United States mortality is substantially lower than mortality in Western Europe and Japan. At age 90, for instance, death rates in Europe and Japan are almost 50% higher than in the Upper Midwest region of the United States, 0.19 vs. 0.13, and about 20% higher than in the Deep South region.

This is remarkable because mortality before age 65 or 70 is substantially higher in the United States than in Western Europe and Japan. Because the very old particularly benefit from medical care and salubrious behavior, it is possible that the U.S. advantage stems from better health conditions for the elderly. The U.S. mortality advantage at older ages might also be at least in part due to the immigration of large numbers of healthy migrants into the United States in the decades before 1920. Another possibility is that conditions during childhood have lingering effects on health at advanced ages: the United States was a world-leader in childhood health at the beginning of this century. In any case, the gap between the United States, on the one hand, and Western Europe and Japan, on the other, is further evidence for the plasticity of mortality at older ages.

Let me now turn to the impact of mortality reductions on the growth of the elderly population, starting with the population of centenarians. In the countries where reliable data are available on centenarians, the number of centenarians is increasing at an exceptionally rapid rate, about 8% per year on average. Demographers are used to population growths rates around 1% per year or so; an 8% growth rate seems more like an inflation rate. In England & Wales, an average of 74 persons per year reached age 100 between 1911 and 1920; by 1990 the number of people celebrating their 100th birthday had increased to almost 2000 and in 1997 the number will be around 3000 (Vaupel and Jeune 1995). In China, Zeng Yi and I estimate that the number of centenarians is doubling every decade. In 1990 there were about 6000 people age 100 and above in China. By the year 2000 there may be more than 12,000.

The population of centenarians is growing, in part, because of the increase in births a century ago, the sharp decline in infant and childhood mortality, and the substantial decline in mortality at ages from childhood up to age 80. Demographic analysis demonstrates, however, that by far the most important factor in the explosion of the centenarian population—two or three times more important than all the other factors combined—has been the decline in mortality after age 80 (Vaupel and Jeune 1995).

Increases in maximum human lifespans are also largely attributable to improvements in survival at the highest ages. Lundström (1995) carefully verified the ages of the oldest people who died in Sweden from 1860 through 1994. In the 30 years between 1860 and 1889, no one survived to age 106. Over successive decades, the maximum gradually rose, with the current Swedish record holder having died at age 112 in 1994. As argued by Jeune (1995), it is possible in Sweden (and other countries with modest populations) that no one attained the age 100 before 1800.

There may have been a few scattered centenarians in earlier centuries, perhaps one per century somewhere or other in the world, perhaps even fewer (Wilmoth 1995). Zhao Zhongwei (1995) presents some evidence, from his study of the genealogy of the Wang family in China, of a man, Wang Xinglian, who may have died at age 102 in the year 1513. Tan Qihua, on the other hand, in some research that has not yet been published, found no plausible examples of centenarians among 4362 famous Chinese who died before 1900 and who are listed in the Dictionary of Historical Chinese Figures. In contrast to the very rare sightings of plausible centenarians in past centuries, fully 100,000 genuine centenarians around the world may be alive to welcome the year 2000 (Vaupel 1994).

Wilmoth's (1995) analysis indicates that “there were almost certainly no true super-centenarians (individuals aged 110 or above) prior to the mortality decline of the past two or three centuries.” Research by Peter Laslett and colleagues suggests that the first reasonably-well-documented case of a super-centenarian is Katherine Plunket, who died at the age of 111 in 1932 (Jeune 1995). Jeanne Calment is the first carefully-verified instance of a person reaching age 120 (Allard, Lebre, Robine 1994); she died at the age of 122 years and 5 months in August 1997.

Centenarians are still unusual and super-centenarians are a thousand-fold rarer, but these findings do illustrate the fact that mortality reduction can have major impacts on population growth at older ages and on extending the frontier of survival. The growth of the population of female octogenarians in England & Wales provides another telling example. The remaining life expectancy of 80-year-old females in England & Wales around 1950 was approximately 6 years. Currently the corresponding figure is about 9 years, some 50% higher. As a result, the population of female octogenarians in England & Wales is roughly half again as big as it would have been if mortality after age 80 had remained at 1950 levels. Putting this in terms of population counts, more than a half million females age 80+ are alive today in England & Wales who would have been dead if mortality after age 80 had not been reduced.*

Table 3 provides information about the size of the older population of various countries, from age 60 and up, for both sexes combined. Estimates are also given for the size of these populations in 2025. The projections assume slow improvements in mortality, so I believe that the estimates for 2025 are likely to prove to be low. Nonetheless, the size of the older population shows substantial increases, not only in Europe but in Japan, the U.S., China, and India as well.

Table 3: Proportion of Population above Age 60 (in %) and Population above Age 60 (in millions) for Selected Countries in 1996 and Projected for 2025.

	% 60+		Millions 60+
	1996	2025	1996	2025
Italy	22	33	13	18
Japan	21	33	26	40
Germany	21	32	17	28
France	20	30	12	18
U.K.	21	29	12	17
U.S.A.	17	25	44	83
China	9	20	115	290
Brazil	7	16	11	31
Mexico	7	13	6	18
India	7	12	62	165
South Africa	7	10	3	6
Egypt	6	10	4	10

Zeng Yi, Wang Zhenglian, and I have recently completed some research on the growth of the old and very old population of China, out to the year 2050 (Zeng, Vaupel, Wang 1997). Under our low-mortality scenario, which I think may capture the decline in death rates in the future, we estimate that the 65+ year-old population of China will grow from 63 million in 1990 to more than 400 million in 2050, a 6-fold increase. For the 85+ population, we estimate growth from 2.3 million in 1990 to more than 80 million in 2050, an extraordinary 36-fold explosion. By the middle of the next century, then, the oldest-old population age 85 and older in China may exceed the total population of Germany.

The multiplication of the population of older people, in China and around the world, heightens interest in a fundamental question: why do some people die at 60, others at 80, and a few at 100? Why are the odds of dying at 80 rather than 60 increasing and the chance of surviving to 100 rapidly increasing (albeit from a very low level)? How important are genetic versus environmental, behavioral, and medical factors in determining how long an individual will live?

It might be expected that the answers to these questions—and the determinants of longevity more generally—are well understood. The duration of life has captured the attention of many people for thousands of years. Lifespans can be readily measured. Huge arrays of vital-statistics data for humans are available for many countries and for many centuries. Masses of longevity and lifespan data are also available for thousands of other species.

A recent review, however, of the determinants of longevity (Christensen and Vaupel 1996) concludes that surprisingly little is known. The chance of reaching age 80 (or 90 or 100) is better for:

Smoking is certainly a health hazard at younger ages and probably at the oldest ages as well. Obesity may be a risk factor and diet more generally is probably important. Some pharmaceuticals, such as DHEA, may increase survival at older ages. Studies of twins and other kinds of related individuals suggest that about 25 percent of the variation in adult lifespans appears to be attributable to genetic variation among individuals (McGue et al. 1993, Herskind et al. 1996). Some research in progress by two colleagues (Anatoli Yashin and Ivan Iachine) suggests that an additional 25 percent may be attributable to non-genetic characteristics that are more or less fixed by the time a person is 30 or so, characteristics such as educational achievement, socio-economic status, mother's and father's age at a person's birth, etc. Research on the relative importance for longevity of various candidate genes and non-genetic fixed-attributes is, however, still at an early stage of development.

Barker's (1992, 1995) “fetal-origins hypothesis” suggests that nourishment in utero and during infancy programs the development of risk factors for several important diseases of middle and old age. Other researchers have also concluded that nutrition and infections early in life have major effects on adult mortality (Kermack, McKendrick, McKinlay 1934, Elo and Preston 1992, Fogel 1993). To the extent this is true, longevity may be determined by conditions in childhood and perhaps before birth. There is, however, conflicting evidence that suggests that current conditions (i.e., at older ages) may be much more important than conditions early in life. Kannisto (1994, 1996) finds period effects to be much more important than cohort effects on mortality after age 80. Christensen et al. (1995) find that from age 6 up to the oldest ages twins (who tend to be born prematurely and at low birth weight) suffer the same age-specific death rates as singletons: this is shown in Figure 7. And Kannisto, Christensen, and Vaupel (1997) find “no increased mortality in later life for cohorts born during famine,” as shown in Figure 8. Pinning down the nature and magnitude of possible lingering effects of early-life conditions on survival at advanced ages is an important research priority.

Figure 7: Male Central Death Rates for Twins and the General Population Born in Denmark 1870-1900.
(Click on figure for full view)

Figure 8: Survival Ratio from Age 17 to 60 and Years Lived after Ages 60 and 80 for Finnish Cohorts Born before, during, and after Famine of 1866-1869.
(Click on figure for full view)

Further insights into the determinants and plasticity of longevity can be gleaned by analyzing the trajectories of age-specific death rates at advanced ages, both for humans and for various non-human species. Benjamin Gompertz (1825) proposed that the force of mortality increased exponentially with age for humans, at least as a serviceable approximation over the range of adult ages for which he had data. Various subsequent researchers, especially in biology and gerontology, have viewed Gompertz' observation as a law that describes the process of senescence in almost all multicellular animals at all ages after the onset of reproduction. As a rough approximation at younger adult ages, Gompertz' exponential formula does capture the rise in mortality in a great variety of species (Finch, 1990).

Demographers have long been interested in the shape of the age-trajectory of human mortality. The general nature of this trajectory from birth to age 80 or so is well known: mortality is high right after birth, falls to a low level around puberty, and then rises more or less exponentially except for some excess mortality among adolescents and young adults. Due to the painstaking efforts of Kannisto (1994, 1996), Lundström (1995; Vaupel and Lundström, 1994), Thatcher (1992), and others, reliable data on mortality after age 80 are now available for Japan and 13 Western European countries. When these data are pooled, it is possible to accurately estimate the age-trajectory of human mortality up to about age 107 for females and age 105 for males. Reasonable estimates can be made up to about age 110, and shakier "guesstimates" can be boldly ventured up to age 120 (Thatcher et al., 1997). Figure 9 clearly shows that human mortality does not increase exponentially after age 80.

Figure 9: Female Central Death Rates at Ages 80 and Over, 1980-1992, for Aggregation of 14 Countries.
(Click on figure for full view)

Source: Compiled by author from data in the Kannisto-Thatcher Oldest-Old Database, Odense University, Denmark. The 14 countries are: Austria, Belgium, Denmark, England & Wales, Finland, France, Germany, Iceland, Italy, Japan, Netherlands, Norway, Sweden, and Switzerland.

Mortality decelerates, rising perhaps to a maximum or ceiling around age 110. Whether mortality is slowly increasing, level, slowly decreasing, or rapidly decreasing after age 110 is uncertain.

These results are based on data on some 70 million humans who reached age 80, some 200,000 who celebrated their 100th birthday, and 1 exceptional person, France's Jeanne Calment, who died at age 122 years and 5 months in August 1997.

Humans are animals. Almost all animals show signs of aging; for almost all animals death rates tend to rise after the age of maturity (Finch, 1990). Even researchers who are only interested in people may benefit from biological insights from studies of other species, because these insights may cast light on the biology of humans. Let me give you just one example.

The largest nonhuman population followed to natural death consisted of 1.2 million medflies studied in a laboratory near Tapachula, Mexico. These flies were held in cages, each holding several thousand flies. As reported by Carey et al. (1992), the trajectory of mortality rises, peaks, and then falls to a low level around which it hovers until the last fly died at an age of 171 days (compared with an average life span in the experiment of 21 days). The results up to day 100 are shown in Figure 10.

Figure 10: Daily Central Death Rates for 1.2 Million Medflies from Emergence to Age 100 Days.
(Click on figure for full view)

Weismann (1889), one of the pioneers of the study of aging, argued that "there is no reason to expect life to be prolonged beyond the reproductive period; so that the end of this period is usually more or less coincident with death" (quoted in Rose, 1991). Charlesworth (1994) and others who helped develop the evolutionary theory of aging have made similar assertions. In the wild there is little egg-laying among medflies after the first month of adult life, so a sharp rise in mortality might be expected around age 30 days. Many of the medflies, however, survived many months after the usual cessation of reproduction. The deceleration of mortality and the concomitant survival of many individuals well beyond the end of the reproductive period has now been observed for every other species for which large populations have been followed to death, including nematode worms and yeast as well as various insects. And Madame Calment lived 122 years, seven decades beyond menopause. A deep relation undoubtedly exists between patterns of reproduction and mortality across species, but simplistic biological models linking the length of the reproductive period and the length of life are unlikely to hold up to close scrutiny.

Mortality deceleration at advanced ages came as a surprise, indeed as a shock, to many biologists and gerontologists. Demographers, on the other hand, had long suspected that death rates probably increased more slowly at older ages, although the data available until recently did not permit a definitive conclusion. In particular the misreporting of age at advanced ages can lead to the false appearance of a deceleration of mortality; age misreporting was very common in earlier centuries and is still common among many populations today (Thoms 1873, Condran, Himes, and Preston 1991, Jeune and Vaupel 1995). Some highly reliable datasets on mortality are now available, however, for many developed countries and for the Han Chinese population as well (Wang, Zeng, Jeune, and Vaupel forthcoming) and they demonstrate that the trajectory of human mortality does indeed fall off from a Gompertz curve (Horiuchi, S., A.J. Coale 1990; Kannisto 1994, 1996; Himes, Preston, and Condran 1994; Thatcher, Kan-nisto, and Vaupel 1997; Vaupel, Wang, and Zeng forthcoming).

Why does mortality decelerate? There are two main explanations. First, all populations are heterogeneous. Some individuals are frailer than others ... and the frail tend to die first. This creates a fundamental problem—indeed it seems to me the fundamental problem—for demographic analyses in general and for analyses of age-trajectories of mortality in particular. The individuals alive at older ages are systematically different from the individuals alive at younger ages. The age-trajectory of mortality reflects both the underlying age-trajectories of mortality for individuals in the population and the effects of compositional change as the frailer individuals drop out of the population.

Some of my colleagues and I have devoted a lot of thought to this problem over the past two decades (e.g., Vaupel, Manton, and Stallard, 1979; Vaupel and Yashin, 1985; Vaupel and Carey, 1993; Wilmoth and Horiuchi, forthcoming). It can be mathematically proven that compositional change (resulting from the higher mortality of the frail) decreases the rate of increase in the age-trajectory of mortality. In fact, even if death rates are increasing with age for every individual in a population, the age-trajectory of mortality can level off or even decline as a result of compositional change. The Gompertz exponential formula could hold for all individuals, even though death rates for cohorts decelerate. A new book by Thatcher, Kannisto, and me (1997) demonstrates that the observed force of mortality for humans after age 80 can be closely fitted by models that assume Gompertz trajectories of mortality for individuals with some heterogeneity among individuals in their frailty.

Such a simple model, however, is unlikely to be the whole truth. Some of the deceleration of mortality at advanced ages may be due to deceleration at the individual level resulting from behavioral and physiological changes that occur with age. Caution is required here, however, because mortality for individuals might actually increase more quickly than a Gompertz curve, which would imply that heterogeneity is even more important in explaining the deceleration of mortality. My colleagues Anatoli Yashin and Ivan Iachine have some evidence from studies of twins that mortality may accelerate faster than an exponential curve for individuals even though mortality decelerates for cohorts. More research is required on the extent to which the deceleration of mortality at older ages is attributable to changes at the individual level versus changes in the composition of the surviving cohort.

Living organisms are complex systems; reliability engineers and systems analysts have learned a great deal about the failure of complex systems. Even the simplest bacterium is more complicated than the most elaborate equipment. Living organisms have repair and homeostatic programs that far excel those in any mechanical device. Nonetheless, it may prove useful to merge perspectives from the study of populations of equipment and the study of populations of people and other forms of life.

Reliability engineers often work with stochastic models in which various states represent the "health" of the system, as determined, for instance, by which components are still working and which components are broken. LeBras (1976) and Gavrilov and Gavrilova (1991) provide some examples that they interpret as models of aging. Yashin et al. (1994) show that the LeBras model and a related model presented by the Gavrilovs produce exactly the same age-trajectory of mortality as does the frailty model proposed by Vaupel et al. (1979). In particular, the various models all lead to a deceleration and eventual leveling off of mortality.

Many biologists seem to believe that it is possible for organisms to approximate the "one-hoss shay" (i.e., horse-drawn carriage) of Oliver Wendell Holmes that ran perfectly until one day when all of its pieces fell apart simultaneously (e.g., Fries and Crapo, 1981; Dawkins, 1995). This is one of the suppositions used to justify the belief that each species, including humans, has a maximum life span. Reliability theory, however, strongly suggests that one-hoss shays are impossible to construct—unless there is built-in time bomb.

Empirical data on the failure of equipment is consistent with reliability theory. Equipment is often designed such that there is a high probability of survival up until some point. The Pioneer space probe, for instance, was designed to reach Mars; consumer durables may be designed to last until the end of the warranty period. Such designs, however, generally result in substantial spans of life after the target age. The Pioneer space probe was still functioning when it escaped the Solar System; some washing machines and refrigerators continue to function well after their warranties have expired. A body design that gives an organism a good chance of surviving long enough to reproduce may be a sufficiently robust design that some of the organisms can survive long thereafter (Hayflick, 1994).

Automobiles are popular pieces of complicated equipment. They are sufficiently standardized that it is meaningfully possible to count their numbers on an age-specific (model-year) basis. Using automobile registration data gathered by the various states of the United States, R.L. Polk and Company did so for July 1, 1941, and then for July 1 of every year from 1947 to the present. These data, which are closely analogous to population count data conducted by national statistical offices and census bureaus, have been assembled and analyzed by myself and C.R. Owens (Vaupel and Owens 1977 and Vaupel 1997). Using standard demographic methods, we estimated, among other summary statistics, the age-trajectory of mortality for automobiles in various cohorts and in various periods. Such age-trajectories for 1970 and 1980 model-year Toyotas and Chevrolets are shown in Figure 11.

Figure 11: Central Death Rates for Chevrolets and Toyotas, 1970 and 1980 Model Years.
(Click on figure for full view)

The deceleration and leveling off of automobile mortality is partially due to heterogeneity. Even among cars of the same make and model year, there are different models and there are differences arising from various errors made in constructing particular cars, from the environment in which the car is driven, from the temperament of the car's owner, etc. Lemons driven on dirt roads by careless, impetuous drivers will tend to be selected out.

Beyond the effects of such compositional change, there are almost certainly physiological and behavioral changes that contribute to mortality deceleration. Older cars are repaired. Older cars may be driven less frequently and more carefully. As cars age, their owners may also age and become more stolid and responsible.

On a more general and speculative level, the question arises—is mortality a property of living organisms or a property of complicated systems? When it comes to death, how do people and flies differ from Toyotas? In particular, is the deceleration and leveling off of mortality a fairly general property of complicated systems? Better understanding of these questions may lead to new insights into aging and survival.

In conclusion, let me reiterate the basic thrust of my talk today. Over the past half century and especially in the most recent decades, remarkable improvements have been achieved in survival at older ages, including and along some dimensions especially at the highest ages. This progress has accelerated the growth of the population of older people and has advanced the frontier of human survival substantially beyond the extremes of longevity attained in pre-industrial times. The widely-held position that mortality at older ages is intractable is untenable. Little, however, is yet known about why mortality among the oldest-old has been so plastic since 1950. There is considerable (but still inadequate) knowledge of why some people die in infancy or childhood and why some people die prematurely at adult ages before age 60 or 70. Much less is known about why some people survive to age 80, others to age 90, and a few to age 100. The little that is known has largely been learned within the past few years and new findings (especially concerning genetic factors) are emerging at a rapid rate. A key finding is that mortality decelerates at advanced ages, not only for humans but for other species of life and for automobiles as well. The deceleration results from some mix of genetic, environmental, behavioral, bio-reliability, and heterogeneity forces and constraints, but the mix is not well understood.

What can demographers contribute to deeper understanding of aging and longevity? As I hope my talk has convinced you, demographers can contribute a great deal. Demography is sometimes defined in a narrow way. The concepts, methods, and materials of demography are so powerful and so useful that it seems to me that it would be better for demography to be defined in a much broader, much more inclusive way. Demography lies at the core of the population sciences and demographers can contribute important research findings to many fields. We understand how to study the structure and dynamics of populations. Our knowledge can help us shed new light on the mechanisms driving population structures and dynamics as well as the consequences of population structures and dynamics. In particular, it seems to me that demographic research will certainly provide new insights and perhaps the crucial insights into the mechanisms that drive the processes of aging and survival.

Finally, let me say again how grateful I am to be here today and how glad I am to have been able to participate in this stimulating IUSSP conference here in China, the site of so much outstanding demographic research. I thank the organizers and our hosts and all of you. Thank you.

* The figure of 9 years for the remaining life expectancy of 80-year-old females in England & Wales is a estimate for 1997, based on data from Kannisto (1996), not a precise figure but good enough for illustrative purposes. Change in life expectancy is often (but not always) serviceable as a rough indicator of the impact of mortality reductions on population size; the required calculations to produce a more exact estimate are fairly complicated. See Kannisto (1996) or Vaupel and Jeune (1995) for details. Kannisto's calculations indicate that mortality improvements after age 80 in England & Wales between 1960 and 1990 (rather than 1950 and 1997) increased the female population by 250,000 persons

Kirill Andreev, Ludmila Andreeva, Dale Kratsch, Tan Qihua, and Wang Zhenglian, at the Max Planck Institute for Demographic Research, made significant contributions to the statistical analyses and graphical presentations in this paper. Much of the research reported is the result of collaborative work with James R. Carey, Kaare Christensen, James W. Curtsinger, Bernard Jeune, Vaino Kannisto, Peter Laslett, Hans Lundström, Kenneth G. Manton, Matt McGue, Cindy R. Owens, A. Roger Thatcher, Anatoli I. Yashin, and Zeng Yi. Some of the research was supported by the U.S. National Institute on Aging through grant P01-08761. Other support was provided by the Danish Research Council and by the Max Planck Society.

Allard, M., V. Lebre, J-M. Robine (1994) “Les 120 ans de Jeanne Calment”, Le Cherche Midi Editeur, Paris.

Barker, D.J.P. (1992) Fetal and Infant Origins of Adult Disease, British Medical Journal, London.

Barker, D.J.P. (1995) “Fetal Origins of Coronary Heart Disease”, British Medical Journal 311:171-4.

Bureau of the Census (1997) “Global Aging into the 21st Century”, Washington, D.C..

Carey, J.R., P. Liedo, D. Orozco, J.W. Vaupel (1992) “Slowing of Mortality Rates at Older Ages in Large Medfly Cohorts”, Science 258:457-461.

Christensen, K., J.W.Vaupel, N.V. Holm, A.I. Yashin (1995) “Mortality among Twins after Age 6: Fetal Origins Hypothesis versus Twin Method”, British Medical Journal 310: 432-6.

Christensen, K., J.W. Vaupel (1996) “Determinants of Longevity: Genetic, Environmental, and Medical Factors”, Journal of Internal Medicine.

Condran, G.A., C.L. Himes, S.H. Preston (1991) “Old-Age Mortality Patterns in Low-Mortality Countries: An Evaluation of Population and Death Data at Advanced Ages, 1950 to the Present”, Population Bulletin of the United Nations 30:21-61.

Dawkins, R. (1995) “God's Utility Function”, Scientific American 273:80-85.

Elo, I.T., S.H. Preston (1992) “Effects of Early-Life Condition on Adult Mortality: A Review”, Population Index 58(2):186-222.

Finch, C.E. (1990) Longevity, Senescence, and the Genome, University of Chicago Press, Chicago.

Fogel, R.W. (1993) “Economic Growth, Population Theory, and Physiology: The Bearing of Long-Term Processes on the Making of Economic Policy”, The Nobel Foundation, Stockholm, Sweden.

Fries, J.F., L.M. Crapo (1981) Vitality and Aging, W.H. Freeman, San Francisco.

Gavrilov, L.A., N.S. Gavrilova (1991) The Biology of Life Span, Harwood Academic Publishers, Chur, Switzerland.

Gompertz, B. (1825) “On the Nature of the Function Expressive of the Law of Human Mortality”, Philosophical Transactions 27:510-519.

Herskind, A.M., M. McGue, N.V. Holm, T.I.A. Soerensen, B. Harvald, and J.W. Vaupel (1996) “The Heritability of Human Longevity”, Human Genetics 97:319-323.

Himes, C.L., S. Preston, G.A. Condran (1994) “A Relational Model of Mortality at Older Ages in Low Mortality Countries”, Population Studies 48:269-291.

Horiuchi, J., A.J. Coale (1990) “Age Patterns of Mortality for Older Women: Analysis Using the Age-Specific Rate of Mortality Change with Age”, Mathematical Population Studies 2:245-267.

Jeune, B., J.W. Vaupel, editors, (1995) Exceptional Longevity: From Prehistory to the Present, Odense University Press, Denmark.

Jeune, B. (1995) “In Search of the First Centenarians” in Jeune and Vaupel (1995).

Kannisto, V. (1994) Development of Oldest-Old Mortality, 1950-1990, Odense University Press, Denmark.

Kannisto, V. (1996) The Advancing Frontier of Survival: Life Tables for Old Age, Odense University Press, Denmark.

Kannisto, V., K. Christensen, J.W. Vaupel (1997) “No Increased Mortality in Later Life for Cohorts Born during Famine”, American Journal of Epidemiology 145(11):987-994.

Kannisto, V., J. Lauritsen, A. R. Thatcher, J.W. Vaupel (1994) “Reductions in Mortality at Advanced Ages”, Population and Development Review 20(4):793-810.

Kermack, W., A. McKendrick, P. McKinlay (1934) “Death-Rates in Great Britain and Sweden: Some General Regularities and Their Significance”, The Lancet 1:698-703.

Kestenbaum, B. (1992) “A Description of the Extreme Aged Population Based on Improved Medicare Enrollment Data”, Demography 29:565-580.

LeBras, H. (1976) “Lois de Mortalite a Age Limite”, Population 31:655-692.

Lohman, P.H.M., K. Sankaranarayanan, J. Ashby (1992) “Choosing the Limits to Life”, Nature 357:185-186.

Lundström, H. (1995) “Record Longevity in Swedish Cohorts Born since 1700” in B. Jeune, J.W. Vaupel (1995).

Manton, K.G., J.W. Vaupel (1995) “Survival after the Age of 80 in the United States, Sweden, France, England, and Japan”, New England Journal of Medicine 333:1232-1235.

McGue, M., J.W. Vaupel, N. Holm, B. Harvald (1993) “Longevity Is Moderately Heritable in a Sample of Danish Twins Born 1870-1880”, Journal of Gerontology 48:B237-B244.

Olshansky, S.J., B.A. Carnes, C. Cassel (1990) “In Search of Methuselah: Estimating the Upper Limits of Human Longevity”, Science 250:634-640.

Rose, M.R. (1991) Evolutionary Biology of Aging, Oxford University Press, New York.

Schächter, F., L. Faure-Delanef, F. Guenot, H. Rouger, P. Forguel, L. Lesueur-Ginot (1994) “Genetic Associations with Human Longevity at the APOE and ACE Loci”, Nature Genetics 6:29-32.

Shrestha, L.B., S.H. Preston (1995) “Consistency of Census and Vital Registration Data on Older Americans: 1970-1990”, Survey Methodology 21(2):167-177.

Thatcher, A.R. (1992) “Trends in Numbers and Mortality at High Ages in England and Wales”, Population Studies 46:411-426.

Thatcher, A.R., V. Kannisto, J.W. Vaupel (1997) The Force of Mortality at Ages 80 to 120, Odense University Press, Denmark.

Thoms, W.J. (1873) Human Longevity: Its Facts and Its Fictions, John Murray, London, England.

Vaupel, J.W. (1977) “Trajectories of Mortality at Advanced Ages” in K.W. Wachter and C.E. Finch (eds.) Between Zeus and the Salmon: The Biodemography of Longevity, National Academy Press, Washington, D.C.

Vaupel, J.W., J.R. Carey (1993) “Compositional Interpretations of Medfly Mortality”, Science 260:1666-1667.

Vaupel, J.W., B. Jeune (1995) “The Emergence and Proliferation of Centenarians” in Jeune and Vaupel (1995).

Vaupel, J.W., H. Lundström (1994) “The Future of Mortality at Older Ages in Developed Countries” in W. Lutz (ed.) The Future of the Population of the World, Earthscan, London.

Vaupel, J.W., K.G. Manton, E. Stallard (1979) “The Impact of Heterogeneity in Individual Frailty on the Dynamics of Mortality”, Demography 16:439-454.

Vaupel, J.W., C.R. Owens (1997) “Automobile Demography”, presented at the XXIIIrd IUSSP General Population Conference, Beijing, China, 11-17 October.

Vaupel, J.W., Z. Wang, Y. Zeng (forthcoming) “Han Chinese Mortality at Older Ages”.

Vaupel, J.W., A.I. Yashin (1985) “Heterogeneity's Ruses: Some Surprising Effects of Selection on Population Dynamics”, American Statistician 39:176-185.

Wang, Z., Y. Zeng, B. Jeune, J.W. Vaupel (forthcoming) “Age Validation of Chinese Centenarians”.

Weismann, A. (1889) Essays upon Heredity and Kindred Biological Problems, Clarendon, Oxford.

Wilmoth, J. (1995) “The Earliest Centenarians: A Statistical Analysis” in Jeune and Vaupel (1995).

Wilmoth, J.R. (1997) “In Search of Limits: What Do Demographic Trends Suggest about the Future of Human Longevity” in K.W. Wachter and C.E. Finch (eds.) Between Zeus and the Salmon: The Biodemography of Longevity, National Academy Press, Washington, D.C.

Yashin, A.I., J.W. Vaupel, I.A. Iachine (1994) “A Duality in Aging: The Equivalence of Mortality Models Based on Radically Different Concepts”, Mechanisms of Aging and Development 74:1-14.

Zeng, Y., J.W. Vaupel, Z. Wang (1997) “Household Projection Using Conventional Demographic Data” in W. Lutz and J.W. Vaupel (eds.) Rethinking Population Projections, forthcoming.

Zhao, Z. (1995) “Record Longevity in Chinese History” in Jeune and Vaupel (1995).