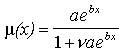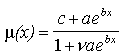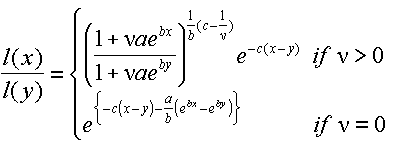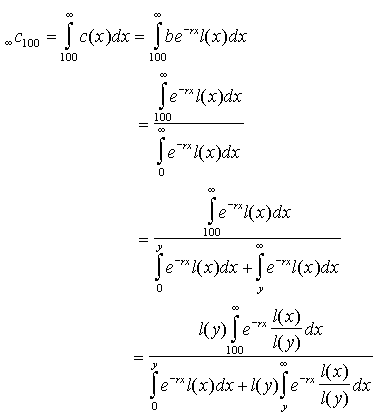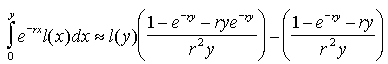The Earliest Centenarians: A Statistical Analysis

When did the first centenarians live? It is well documented that the number of centenarians in industrialized countries has increased dramatically during this century (Kannisto 1988, Thatcher 1981, 1992, Vaupel and Jeune, this monograph). Is it conceivable that at some earlier moment in human history there were no individuals who achieved this milestone age? Or, to borrow a phrase from Vaupel and Jeune, when did the "emergence of centenarians" occur? Are centenarians a product of the enormous mortality decline that accompanied industrialization?

Some authors have speculated that centenarians may have been rare or even non-existent prior to the industrial era. For example, based on the observed trend in the maximum reported age at death in Sweden during 1861-1990, Wilmoth and Lundström (1995) speculated that "true centenarians may have been quite rare in the pre-industrial period." Similarly, Jeune (1994 and this monograph) put forth the more daring hypothesis that no humans lived to age 100 before 1800, or to 110 before 1950. Unfortunately, direct tests of these hypotheses are nearly impossible, since accurate records of age at death are usually available only for modern populations. In this chapter we attempt to test these hypotheses using statistical models based on plausible scenarios of adult mortality in the period prior to the mortality decline of the past 250 years.

To accomplish this task, we must address several preliminary questions. First, in the absence of direct evidence, how can the concept of the "emergence of centenarians" be defined and operationalized in a practical yet meaningful fashion? Second, how can we model the age pattern of pre-industrial mortality, especially in the late adult age range (since this is the age range that most affects the probability of survival to age 100)? Third, what are plausible levels and patterns of pre-industrial mortality?

In this chapter, we propose two definitions of the "emergence of centenarians" and demonstrate that our predictions about the timing of that emergence are similar for both definitions. We also suggest that the age pattern of adult mortality can be modeled using the Gompertz-Perks family of curves. We derive evidence about the levels and patterns of pre-industrial mortality from a detailed analysis of model life tables and from a review of existing studies of high-mortality populations.

Combining these various components, we conclude that it is likely that the emergence of centenarians preceded the industrial revolution by several thousand years. There is very little evidence to suggest that the trend in human life expectancy rose (or fell) significantly during the agricultural era. Therefore, the emergence of centenarians during this period must be attributed to the gradual rise in population size, which slowly increased the probability that centenarians, although extremely rare worldwide, should have been observed with some minimal regularity. So defined, our best guess is that the emergence of centenarians occurred once world population rose to about 100 million around 2500 B.C. at the time of the first great civilizations of the ancient world.

Given complete and accurate information about the lifetimes of all individuals who have ever lived, it would be possible to identify a precise date when the first person attained the age of 100 years. Lacking this information, however, we must resort to statistical models that allow us to predict when the earliest centenarians might have lived. These models can not yield precise dates for exact events. Rather, they are used to derive the probability of a given event or an expected number of occurrences within a specified time period.

From a historical perspective, we might say that the emergence of centenarians occurred once the probability that all subsequent birth cohorts should have yielded at least one centenarian was above some level. This definition still requires important choices, however. Do we mean single-year or 100-year birth cohorts, for example? And do we want to require that the event occurs with at least even odds (pł 0.5) or with virtual certainty (pł 0.99)? In our calculations, we discovered that the latter choice was not terribly important: most models that offered even odds (or better) of at least one centenarian per cohort predicted, moreover, that a centenarian would be observed with virtual certainty. Thus, we chose the stricter requirement.

The choice of a cohort boundary was more arbitrary. We reasoned that the relevant issue was when centenarians became sufficiently common that they would have been observed at least on occasion worldwide, and it seemed reasonable to equate "on occasion" with "at least once per century". Thus, we propose to examine whether, during a given era, it is likely that there would have been at least "occasional centenarians." Formally, we will state that there were occasional centenarians in some time period if, for a given model of mortality and estimated population size, the probability of observing at least one centenarian per century was 0.99 or more. This definition does not insure that there would always have been one living centenarian on the planet. It does mean, however, that the folklore of a single person who was reputed to have attained this age could not be dismissed as utterly implausible (although it might still be correct to dismiss a multitude of such reports as fallacious). It also means that the phenomenon of being a centenarian was never too far (in a temporal sense) from any living human during this time period.

With this definition, we still face an additional complication due to the fact that multiple mortality scenarios may be considered plausible for a given historical period. Also, although it is substantially less important than the mortality regime, we can estimate the historical size of the world population only within a range. It is possible, therefore, that we could have a number of conflicting indications about whether there were occasional centenarians in some time period. For this reason, in order to assert that centenarians had emerged by some date, we require that there be a "preponderance of evidence" for occasional centenarians from that time onward. Specifically, when considering multiple mortality scenarios, we require that three fourths of them provide a positive indication for occasional centenarians in order to proclaim the emergence of centenarians.

Thus, our first definition of the emergence of centenarians can be summarized as follows: the historical emergence of centenarians is said to have occurred if a preponderance of the available evidence (at least three quarters of the plausible mortality scenarios) indicates with virtual certainty (p 0.99) that centenarians must have been observed at least occasionally (no less than once per century).

A second definition of the "emergence of centenarians" relies on the expected number of living centenarians, rather than the probability of survival within a cohort. One reasonable criterion for "emergence" is to require that the expected number of centenarians in the world be at least one. Clearly, this criterion is more strict than requiring at least one centenarian per century. Again, we will consider a range of plausible mortality scenarios, and we will require a "preponderance of evidence" as proof of the "emergence of centenarians."

Using stable population theory, it is possible to compute the expected prevalence of centenarians in the population for a given mortality scenario. Multiplying this number by the estimated population size gives the expected number of living centenarians. Because it is based on a single number (either the prevalence estimate or the expected number of centenarians) rather than a dichotomous indicator variable, this definition is somewhat more amenable to simulation studies than the first definition. A range of plausible mortality scenarios produces a distribution of prevalence estimates. If three quarters of the prevalence estimates predict at least one centenarian in a given time period, then we say, by our second definition, that the emergence of centenarians has occurred.

In order to model the probabilities or expectations described in the previous section, we need a model of adult mortality. All mortality curves considered in this chapter fall within the Gompertz-Perks family. This choice can be justified by a combination of theoretical arguments and empirical evidence.

where a > 0 and b > 0. The Gompertz curve represents the age-dependent component of mortality and is justified, in part, by the statistical theory of extreme values (Gumbel 1937, 1958, Aarssen and de Haan 1994). When plotted in a logarithmic scale, the Gompertz curve rises linearly with age (Figure 1a), thus mimicking one of the most commonly observed features of empirical mortality curves.

In Makeham's formula, a small modification consists of adding a constant parameter to the Gompertz curve:

where c ł 0. The constant, c, represents the level of "background mortality" that is the result of age-independent risks (Gavrilov and Gavrilova 1991, Horiuchi and Wilmoth 1994). Compared to the Gompertz curve, the Makeham curve bends upward at lower ages because it is bounded by a lower asymptote of c (Figure 1b). The importance of the background mortality constant in models of human mortality is well documented. Even Gompertz had speculated about the existence of this second component of adult mortality (Jordan 1975). In recent empirical work, furthermore, it has been demonstrated that a decrease in the age-independent background component has been a major contributing factor to the overall decline of adult mortality during the last century (Gavrilov and Gavrilova 1991).

At the highest ages, it is now well-documented that mortality curves tend to rise less than exponentially (Horiuchi and Coale 1990, Kannisto 1994), suggesting a logistic form, such as contained in Beard's formula:

where n ł 0. Such a form for the mortality curve is also justified by theoretical arguments, whereby the less-than-exponential increase at advanced ages may reflect either the influence of population heterogeneity and differential selection, or the workings of a multiply redundant system (Yashin et al. 1993, Gavrilov and Gavrilova 1991, Horiuchi and Wilmoth 1994). Compared to Gompertz' law, the Beard formula produces a curve that bends over at advanced ages, bounded by an upper asymptote of 1/n (Figure 1c).

This formula produces a curve that deviates from the Gompertz at both younger and older adult ages (Figure 1d). The Perks' curve contains an inflection point in late adulthood that should move upward as mortality falls (Horiuchi and Wilmoth 1994). The graphs shown in Figure 1 are drawn using the average values of these four parameters for the simulations of the base model described later in this chapter.

The full Perks formula contains 4 parameters, a, b, c, and n. Two of these have fairly direct interpretations: c represents the level of background mortality, 1/n gives the upper asymptote of the mortality curve, and both are expressed in terms of the force of mortality, m(x), in its original scale. The Gompertz parameters, a and b, on the other hand, are more abstract: b is the rate of exponential increase in mortality across the age range in the Gompertz model, but this interpretation is only approximate in the Makeham, Beard, or Perks models; a is the exact force of mortality at age 0 only in the Gompertz model, but even this fact does not aid in interpretation since the model applies to adult mortality alone.

In choosing the input assumptions for the model, it seemed judicious to reparametrize this model so that all 4 parameters lend themselves to more direct interpretations. Since age 50 was (arbitrarily) chosen as a starting point for our models of late adult mortality, e₅₀ (remaining life expectancy at age 50) and ₅m₅₀ (the death rate between ages 50 and 55) were chosen as alternatives for a and b in the above model. Using numerical methods, it is possible to find the unique parameters, a and b, in the above formulas that reproduce a given e₅₀ and ₅m₅₀ (for fixed levels of c and ).¹ Thus, all model assumptions for this study are expressed in terms of e₅₀, ₅m₅₀, c and n.

Having chosen a family of mortality curves, it is also necessary to examine existing evidence regarding mortality levels and patterns during the pre-industrial period. For example, what were typical values of life expectancy at birth or at age 50? Was the age pattern of mortality similar to what we observe in modern life tables? Is there evidence of a secular trend in mortality levels prior to the enormous decline of the past 200 or 300 years?

It is surely accurate to state that none of these questions can be definitively answered, at least based on evidence now available. Furthermore, it is not the purpose of this study to add to the existing body of evidence about pre-industrial mortality levels. Rather, our purpose in this section is to review the available evidence and to extract from it reasonable conclusions about pre-industrial mortality levels and patterns to serve as the basis for the present inquiry. We will draw our mortality assumptions from a combination of sources. In this section, we examine evidence about mortality levels in populations at historically low levels of life expectancy. In the following section, we analyze data from two collections of model life tables to derive relationships that help to determine the age pattern of mortality.

Regarding mortality levels, Table 1 brings together a number of estimates of life expectancy (both at birth and at age 50) in high-mortality populations from a variety of sources. While we believe that this evidence provides a reasonable justification for the assumptions about pre-industrial life expectancy adopted in this chapter, we also acknowledge that the conclusions of this study may need to be revised at some future date if different and better evidence becomes available.

There have been several notable attempts to trace pre-industrial trends in morbidity and mortality. Reliable written records that could be used to document historical mortality patterns are lacking for almost all large populations prior to the industrial period. Historical demographers, however, have attempted to reconstruct various populations using religious or genealogical records. For example, Hollingsworth (1977) computed life tables for the British peerage beginning with the cohort born in 1550 (see Table 1). More recently, Lee et al. (1993) made mortality estimates for the Qing imperial lineage (1644-1911), and Zhao (1994) calculated life tables for the Wang dynasty during 0-1760 A.D. (Lee and his colleagues present their results in graphical form only, and thus we give them here as a range of values with an indication of the long-term trend.) Although these groups may not be representative, the evidence from these studies of elites provides clues about what the mortality experience of the general population may have been.

Another approach for estimating pre-industrial mortality levels and patterns is based on paleodemographic data (mostly, from studies of skeletal remains). The most extensive work in this area is the book by Acsadi and Nemeskeri (1970), which contains life tables for a variety of populations, from early hunter-gatherers to modern industrial societies. Table 1 in this chapter presents life expectancies for populations from four pre-industrial periods (Stone Age, Copper Age, Roman era, and Middle Ages). From among the various tables presented in Acsadi and Nemeskeri's book, here we consider four that were judged to be among the most reliable (Thatcher 1980). Nevertheless, the mortality levels given here may not be typical of the entire time period in question. For example, the Stone Age population with an estimated life expectancy of 21 years was unearthed at two cemeteries on the Maghreb region in Morocco and Algeria. There it appears that burial practices were stable over a period of two centuries, so it may be reasonable to conclude that the paleodemographic data provide an accurate picture of the mortality of that population. A stable community that survived so long during this time period was likely to be advantaged, however, so Acsadi and Nemeskeri reckon that average Stone Age life expectancies were probably lower than 21 years (a conclusion that may or may not be correct).

There are several reasons to be cautious about interpreting literally life tables constructed from paleodemographic data (Sattenspiel and Harpending 1983, Johannson and Horowitz 1986, Paine 1989, Wood et al. 1992). Probably the two most important for our purposes are the problems of selection bias and non-stationarity. As suggested above, populations for which reliable paleodemographic data are available may tend to be an advantaged or otherwise unrepresentative sample. Non-stationarity results in biased estimates of life expectancy insofar as the real distribution of deaths in the population does not mirror the hypothetical distribution of deaths in the life table. A population with a stable positive growth rate, for example, would have an average age at death that is lower than the life expectancy of the average individual.

Although these biases may be severe, it is also possible that they may tend to cancel each another. If availability of apparently reliable paleodemographic data is a marker of an advantaged society, then that advantage may be reflected in both lower mortality and a positive growth rate. While the former would contribute to an overestimate of average life expectancies, the latter would lead to an underestimate. It is difficult to speculate without further investigation about whether these two biases might be of similar magnitude. This argument does suggest, however, that paleodemographic studies, in spite of their obvious flaws, may still provide a useful indication of pre-industrial life expectancies.

In speculating about pre-industrial mortality levels, it is also useful to make comparisons to high-mortality populations from more recent times. For this purpose, Table 1 presents data from Indian life tables during the late 19th and early 20th centuries (Davis 1951), as well as estimates for three 19th-century slave populations (John 1988, Roberts 1952, Koplan 1983). The table also gives mortality estimates for a unique group of freed American slaves who returned to Africa to build colonial settlements in Liberia (McDaniel 1992). Life expectancy at birth for these Liberian immigrants is the lowest ever recorded for a human population, due apparently to the enormous toll of tropical diseases for which the immigrants lacked immunity. When life expectancies are calculated conditional on surviving a full year after immigration, however, the Liberian levels are much closer to those observed in other high-mortality populations (at least for life expectancy at birth, e₀). Finally, Table 1 also gives life expectancies for Sweden during 1751-1760, around the beginning of the industrial era, from Breslau during 1687-1691 (Halley's life table), and from England and Wales and the city of Liverpool during 1841 (except the Swedish data, these figures come from Thatcher 1980).

It is difficult to find clear evidence in Table 1 of long-term changes in mortality levels prior to 1600 A.D. Mortality declines during recent centuries are evident in the data for the British peers, the Qing imperial line, and India. For the British peers, this decrease is apparently concentrated in the adult ages, while for the Qing, infancy and childhood appear to have been main loci of change. Over a much longer and earlier time period, however, data for the Wang clan show no evidence of a secular mortality decline. Unfortunately, the genealogical data used in the latter study contain incomplete records of infant and childhood deaths, so reliable estimates of life expectancy at birth are not available. Still, it is worth noting that the absence of a long-term trend in Wang mortality during 0-1760 A.D. is indicated for all ages above 20 years (Zhao 1994).

Thus, although the mortality decline of the past few centuries has been dramatic, there appears to be no solid evidence of significant long-term changes in human life expectancy prior to the 17th century. Cohen (1989) argues eloquently that human health and mortality deteriorated following the transition to agriculture that began around 8000 B.C., although other scholars offer a more cautious interpretation of the existing evidence (Wood et al. 1992). During the succeeding 10 millenia, there appear to be no compelling arguments regarding the long-term trend in human mortality prior to around 1600. It is certain that mortality levels fluctuated widely during this period (Flinn 1981), but the evidence, flawed though it may be, provides little suggestion of a long-term trend either upward or downward.

If we accept the theory that mortality trends were essentially flat during most of the agricultural era, we are still faced with the problem of determining the prevailing average level of life expectancy. Based on Table 1, we have adopted a working assumption that the worldwide e₅₀ during the agricultural era averaged around 14 years. It seems conceivable that this estimate could be off by a few years in either direction, or that there could have been periodic swings in mortality levels lasting a century or more. Therefore, our analyses in succeeding sections of this chapter always consider a range of plausible life expectancies. Given the available evidence, however, it seems unlikely that e₅₀ on a world scale would have dipped below 9 years or risen above 19 years for extended periods during this era.

The justification for assuming that e₅₀ had an average value around 14 years in the agricultural era is imperfect but, on balance, a seemingly reasonable conclusion. A simplistic argument is that e₅₀ must have averaged around 14 years since that value lies at the midpoint of the range of available estimates (roughly, from 9 to 19 years).

Nevertheless, some of the evidence in Table 1 might suggest that typical values of e₅₀ were lower than 14 years. For example, among the results from Acsadi and Nemeskeri, only the Roman life table has an e₅₀ above 12 years, but the residents of the Roman empire may have enjoyed an unusually advantageous health environment compared with surrounding peoples and time periods. Thus, the lower values of e₅₀ found in the tables for the Copper Age and the Middle Ages could represent more typical levels of pre-industrial life expectancy.

It is quite questionable whether all of the estimates of e₅₀ in Table 1 should be read literally, however. In particular, the estimates based on skeletal remains are suspect, since apparently the techniques of age imputation on which they rely produced no evidence of very old individuals. Thus, the life tables for the Stone Age, the Copper Age, and the Middle Ages referred to in Table 1 indicate a zero probability of surviving past ages 78, 76, and 85, respectively. It is worth mentioning that, among the four sets of life expectancies in Table 1 taken from Acsadi and Nemeskeri (1970), only the Roman set was not based on skeletal remains. Rather, this Roman era life table was constructed from tombstone epitaphs and contains a maximum age at death of 100 years. It is less surprising, then, that it alone among these four contains a higher estimate of e₅₀.

We might also argue that the results in Table 1 are biased because elite populations are over-represented. For example, some of the highest estimates of adult life expectancies during the agricultural era are found in the life tables for the Wang dynasty, but these pertain to an elite population whose mortality experience may have been atypical compared to the overall population.² On the other hand, the earliest mortality estimates for the British peerage, another elite group, contain an e₅₀ of only about 12 years. Therefore, the mortality experience of elites is not necessarily more favorable than the average.

A further piece of evidence that e₅₀ should have averaged around 14 years during the agricultural era comes from combining direct mortality estimates with information from model life tables. For example, Table 2 shows the values of e₀ and e₅₀ contained in Coale-Demeny model life tables at low levels (Coale and Demeny 1983), and in an alternative set of model life tables constructed by Preston et al. (1993). If we believe that agricultural e₀ was centered in the low to mid twenties (and almost all the available evidence is consistent with this conclusion), then the Coale-Demeny model life tables indicate that e₅₀ should have been around 14 years or slightly higher.

At these low levels of life expectancy, however, the Coale-Demeny model life tables are the result an extrapolation from life tables at much higher levels of life expectancy. Indeed, the lowest levels of e₀ in the tables used to construct this set of model life tables were 33.4 years for males and 35.5 years for females (Preston et al. 1993). Thus, the relationships between e₀ and e₅₀ in very high mortality populations may be poorly represented by these tables. Some authors have argued, in particular, that the Coale-Demeny tables may overestimate infant mortality at low levels of life expectancy and simultaneously underestimate adult mortality (Bhat 1987, Preston et al. 1993). Thus, the values of e₅₀ for the Coale-Demeny tables in Table 2 may be too high relative to e₀.

A new set of model life tables, however, seeks to correct this imperfection. Preston et al. (1993) computed model life tables at low levels of life expectancy based on interpolation between the raw Liberian life table described earlier (with extremely low life expectancies, as seen in Table 1) and the United Nations General mortality pattern with e₀ = 35. The relationship between e₀ and e₅₀ for these tables is also shown in Table 2. From these results, if e₀ was around 24 years, then e₅₀ should have been around 14 years. Furthermore, in order to obtain an e₅₀ as low as 12 years, these model life tables suggest that the average male-female e₀ would need to be around 15 years, a value that seems unrealistically low based on all available historical evidence. In conclusion, then, the evidence from model life tables seems to provide additional support for our assumption that agricultural levels of e₅₀ should have been around 14 years on average.

As stated earlier, however, the purpose of this investigation is not to resolve the issue of mortality levels and trends during the agricultural era. Rather, our strategy here is to use existing evidence to derive plausible input assumptions for our models of centenarian prevalence. If these assumptions prove to be incorrect upon consideration of further evidence, the results presented here could simply be modified using the same model with new inputs. Furthermore, since we employ a range of assumptions in this chapter, the reader has the opportunity to arrive at different conclusions without making additional calculations.

Aside from the question of mortality levels, it is also necessary to make assumptions about the relationships that determine the age pattern of mortality. In the Gompertz-Perks model, the mortality curve is fully specified only when a chosen value of e₅₀ is accompanied by assumptions regarding ₅m₅₀, c, and n. Three of these parameters, e₅₀, ₅m₅₀, and c, tend to be strongly correlated, so they must be chosen in a manner to insure that the resulting mortality curve is plausible. That is, in most known life tables, a given level of e₅₀ tends to be associated with a fairly narrow range of values for ₅m₅₀ and c. If these correlations are ignored in choosing the input parameters, the curve that results may be quite different in character from anything we have thus far observed in populations for which reliable data are available.

Of course, it is possible that mortality curves for pre-industrial populations differed in fundamental ways from the more recent life tables that form the basis of our experience in these matters. In this study, however, we assume that early life tables share the same kinds of empirical relationships between the parameters of the Gompertz-Perks family that are observed in modern life tables. These relationships can best be derived through an analysis of model life tables and are expressed here by a series of regressions. These regression are used to guide the choice of model parameters in the analyses of the following sections.

The two most commonly used sets of model life tables are the Coale-Demeny and U.N. collections (Coale and Demeny 1983, United Nations 1982). Both were developed based on observed empirical relationships among life tables constructed from what were thought to be reliable data. Both collections of model life tables contain a handful of "regions" or "patterns," which represent different typical age schedules of mortality. The Coale-Demeny system contains four regions: North, South, East, and West. The U.N. system contains five patterns: Chilean, Latin American, Far Eastern, South Asian, and General.

As noted earlier, however, few of the life tables used in constructing these two sets of model life tables displayed overall levels of mortality that would be considered very low by historical standards. Among the input tables for the U.N. set, the lowest life expectancies at birth were 37.6 (males) and 40.1 (females). Coale and Demeny had only a few reliable observations of mortality at lower levels of life expectancy: the lowest levels of e₀ in their input tables were 33.4 years for males and 35.5 years for females (Preston et al. 1993). In contrast, it is generally assumed that life expectancy in the pre-industrial era was centered in the low to mid twenties (see previous section). Thus, the model life tables used for guiding our choice of model parameters are already based, in part, on extrapolations of the age pattern of mortality outside the range of reliable life tables.³

Our first task is to choose values of ₅m₅₀ and c for a given level of e₅₀. Figure 2 demonstrates the inverse log-linear relationship that is typical for e₅₀ and ₅m₅₀. This graph also shows the linear regression of the model life table values of log(₅m₅₀) on e₅₀. The analysis is restricted to model life tables with e₀ below 40 years for the U.N. tables, or levels 1-9 for the Coale-Demeny tables. The data points for females are indicated by upper-case letters; for males, by lower-case letters. This regression explains 84 percent of the original variance in log(₅m₅₀). Three lines are shown in Figure 2: the OLS regression line, and this regression line plus and minus the maximum residual from the regression. In the analyses that follow, the choice of ₅m₅₀ for a given e₅₀ is centered around the value given by this OLS regression line. Alternate values are expressed as the regression estimate plus or minus some proportion of the maximum residual.⁴

The method for choosing values of the background mortality parameter, c, is somewhat more complicated, because it involves a multiple regression. Figure 3 shows simple scatter plots of c against both e₅₀ and ₅m₅₀.⁵Neither of these pairs are as strongly correlated as e₅₀ and log(₅m₅₀) (the correlation coefficients are -0.72 for e₅₀ and c and 0.85 for log(₅m₅₀) and c, compared to 0.94 for e₅₀ and log(₅m₅₀)). The best prediction is achieved by regressing c on both e₅₀ and ₅m₅₀, although such a model still only explains 77 percent of the original variance. In some of the analyses that follow, the value for c is assumed to equal either this regression estimate, or the estimate plus or minus some proportion of the maximum residual from the regression.

The fourth parameter of the Gompertz-Perks mortality model, n, determines the upper asymptote of the mortality curve. Unlike the other parameters, however, the values of n that were found by fitting the Perks formula to model life tables did not demonstrate significant or meaningful correlations with the other parameters. In any case, these estimated values of n should not be viewed as reliable, since they are based on model life tables with limited detail regarding the age pattern of mortality in the age range where the effects of this parameter are most evident, in particular, above age 90 or 100. For this reason, in the following analyses, the parameter n was chosen in a more arbitrary fashion, based nevertheless on empirical evidence about typical values of this parameter derived from modern, low-mortality populations.

A fifth mortality parameter is needed when we calculate estimates of centenarian prevalence. Because the Gompertz-Perks model is valid only in the adult age range (in our usage, above age 50), we also need an estimate of survivorship at younger ages. Using standard notation, let l(50) be the proportion surviving from birth to age 50. As before, to obtain a "best estimate" of l(50) (conditional on e₅₀, ₅m₅₀, and c) we will rely on a regression equation derived from model life tables at low life expectancies. In simulations, the chosen value of l(50) will equal this estimate plus or minus some multiple of the maximum residual from the regression analysis. One complication, however, is that we dropped the life tables for the U.N. Far Eastern pattern before fitting the regression model, since the relationship between l(50) and the other parameters is quite atypical in this case: the values of l(50) for the Far Eastern tables are unusually high, so including them in the model shifts the regression estimate upward and produces rather large residuals. It was thus convenient to eliminate the Far Eastern tables from the main analysis and later to test the importance of this simplification in a sensitivity analysis.

The first question that we will address in this chapter can be stated as follows: Is it plausible that there were individuals who attained the age of 100 years, at least on occasion, during the long period of human history from the Agricultural to the Industrial Revolutions? As a shorthand for this question, we are looking for evidence of an "occasional centenarian" during this period. There is very little reliable historical documentation from this period that might definitively resolve this issue. Thus, our investigation will be based on statistical models, which are used to assess the plausibility that at least a few individuals, on a worldwide basis, might have attained the milestone age of 100 years prior to around 1700.

There are various means of defining, formally, what is meant by the phrase "an occasional centenarian." Statistical models of the kind described in the previous section all yield non-zero estimates of the probability of survival to age 100, and thus they produce non-zero estimates of the expected number of centenarians (however defined) as well. We must choose a threshold level for the probability of observing at least one centenarian during some period. As discussed previously, it seems reasonable to assert that an "occasional centenarian" would mean that at least one person had attained this age (worldwide) during a given century.

Accepting the arbitrary nature of these choices, we thus propose the following formalization of the notion of an occasional centenarian. Let X be a random variable representing the number of individuals who attain age 100 during a given century. Then, for a given mortality scenario, we will say that there is an occasional centenarian during that century if

. In a Poisson probability model, this requirement implies that the expected number of centenarians during this period is at least 4.6. In other words, an average of 5 or more centenarians every 100 years is almost certain to yield at least one centenarian per century.

Figures 4 , 5, 6 summarize the results of this analysis. A brief outline of the steps taken to produce a single data point in Figures 4, 5, 6 is given below, followed by a more detailed description of each step:

1.	Choose a set of four input parameters (e₅₀, ₅m₅₀, c and n), limiting the choice of input parameters to values that may be considered at least weakly plausible based on mortality patterns in model life tables and other sources.
2.	Convert e₅₀ and ₅m₅₀ to a and b (holding c and n constant).
3.	Using the Gompertz-Perks model, compute the probability of survival from age 50 to 100, thus l(100) / l(50).
4.	Choose an assumption for the initial population size, called N₅₀, which equals the estimated number of persons who attain age 50 (worldwide) during a given century.
5.	Following the binomial model, compute the expected number of survivors to age 100, called l, out of the initial cohort of N₅₀. Thus, .
6.	Following the Poisson model, compute the probability of at least one surviving centenarian out of an initial cohort of N₅₀ individuals, thus 1 - e^-l. If this probability exceeds 0.99, then a dot corresponding to the assumed parameter values is plotted in Figures 4, 5, 6 in the appropriate location.

The decision to limit assumed values of e₅₀ to the range of 9-19 years was based on the evidence presented earlier, which shows that this range includes almost all plausible estimates of mortality levels above age 50 in agricultural populations prior to the mortality decline of the industrial period. We use model life tables to guide our choice of ₅m₅₀ and c for a given level of e₅₀. For each value of e₅₀, seven levels of ₅m₅₀ were considered: the regression estimate (see previous section) plus or minus 0.5, 1, or 1.5 times the maximum residual from the regression.

The choices of c used in constructing Figures 4, 5, 6 are based partly on the regression model of the previous section and partly on a simpler strategy for obtaining an assumed value of the background mortality parameter. Regression values plus or minus some multiple of the maximum residual sometimes yielded implausible, or even impossible (i.e., negative), values of c. For this reason, one set of calculations in Figures 4, 5, 6 is based on the exact regression estimates of c. The other three sets of calculations assume that c is some fixed proportion of the mortality rate between ages 50 and 55, ₅m₅₀. For the model life tables considered here, this proportion varies from a minimum of 9 percent to a maximum of 63 percent. Thus, calculations based on assumed proportions of 5 and 65 percent represent the extremes of plausibility, while 35 percent is an intermediate value. By choosing the values of c in this fashion, we are also better able to consider the impact of this background mortality parameter on calculated survival probabilities.

The last parameter to be chosen, n, determines the upper asymptote of the mortality curve. As noted before, this asymptote equals 1/n. Setting n= 0 implies that mortality increases in an exponential fashion (hence, with no upper limit) at the highest ages. Setting n= 1 implies that the upper asymptote of the µ(x) curve equals one. The values of used here can safely be thought to cover the range of plausible levels of this parameter. An upper asymptote of one is a fairly reasonable assumption based on available empirical evidence, although it is important to bear in mind that such evidence that exists is derived from modern, low-mortality populations. The assumptions,n = 0.5 and n = 1.5, are probably already sufficiently extreme that they cover the plausible range of human experience. The assumption, n= 0, is included mostly for comparison purposes and seems much less likely based on evidence from modern life tables.

Numerical methods were used to convert e₅₀ and ₅m₅₀ into a and b (for given values of c and n). In brief, the value of b is found by a numerical search algorithm to match the assumed value of e₅₀. On each iteration, the value of a given b is obtained using equation (4) and assuming that µ(52.5) = ₅m₅₀.

The probability of survival from age 50 to 100, thus l(100) / l(50), is calculated using the following formula:

Assumed population sizes are based on those given in Durand (1977) and shown in Table 3. It is necessary to convert estimates of total population size into N₅₀, which equals the estimated number of persons who attained age 50 during a given century. Three periods were selected for this analysis: circa 8000 B.C., corresponding (roughly) to the beginning of the agricultural era; circa A.D. 0-14, during the Roman Empire; and the 17th century, just prior to the Industrial Revolution.

It is clear from a comparison of Figures 4, 5, and 6 that these calculations are not terribly sensitive to differences in population size: even the very large differences in base population between these three time periods yield rather small differences in the probability of observing an occasional centenarian (in case it is not obvious to the reader, the differences between these three figures are due entirely to differences in assumed population size). Similarly, all plausible population estimates for a single time period produce nearly identical results, so we can comfortably choose a single set of estimates and not worry about the sensitivity of the results to this one parameter choice.

To obtain an assumed value of N₅₀ for each time period, we began by observing that the proportion of a population that is age 50 lies within a fairly narrow range under a variety of plausible assumptions about mortality levels and growth rates. For example, considering all model life tables in the Coale-Demeny system with e₀ between 20 and 30 years, and allowing the growth rate in a stable population to fluctuate between -0.5 and +1 percent, the number of individuals who are aged 50 as a proportion of the total population lies in a range of 0.64 to 1.2 percent (the details of these calculations, based on Coale and Demeny 1983, are available from the author upon request). For a single estimate, therefore, it seems reasonable to assume that the number of individuals attaining age 50 in a single year equals 0.9 percent of the average total population for that year. For this analysis, however, we have defined N₅₀ to be the number of persons who attain age 50 over the period of a century. Thus, multiplying by 100, we will assume that N₅₀ equals 0.9 multiplied by the average total population during the century.

For the three time periods in question (circa 8000 B.C., circa A.D. 0-14, and the 17th century), we assume that the average total population size was 8, 300, and 700 million persons (see Table 3). Thus, N₅₀ for these three periods was taken to equal 7.2, 270, and 630 million persons. Although these estimates must be considered very rough approximations, they are adequate given the minimal sensitivity of the results to this particular assumption.

Calculation of the estimated number of centenarians out of an initial cohort of N₅₀ persons is straightforward using the binomial probability model. In this instance, the probability of survival is l(100) / l(50), and thus the expected number of centenarians, l, equals 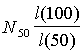step4.gif (1169 bytes)

The Poisson model provides a convenient and accurate approximation to the binomial in situations where the population size is large and the probability of "success" is small. Given l, the expected number of centenarians, the probability of observing at least one centenarian equals 1 - e^-l. If this probability exceeds 0.99, then a dot corresponding to the assumed parameter values is plotted in Figures 4, 5, 6 in the appropriate location. These figures are drawn in a way that allows us to observe the importance of all four parameters of the Gompertz-Perks mortality model. Each figure contains four graphs, which differ among themselves in the manner of choosing the background mortality parameter, c. In addition, for each combination of e₅₀ and ₅m₅₀ in these graphs, there may be up to four points representing four assumed values of the parameter n(these four points are centered around the assumed value of e₅₀, which in all cases equals a whole number value between 9 and 19 years).

The purpose of Figures 4, 5, 6 is to provide information about the mortality conditions that would have been necessary in a given era to yield an occasional centenarian, without yet speculating in a precise manner about what those mortality conditions were. At this point, we are asserting only that overall mortality levels above age 50 in these periods were probably in a range to produce an e₅₀ between 9 and 19 years, with associated levels of ₅m₅₀, c, and n as depicted in these graphs. These three figures make it clear, therefore, that our ultimate conclusions about the existence of occasional centenarians in the pre-industrial era will depend on our assumptions about the actual levels of mortality within this broad range.

These figures provide an illustration of the role of the various model parameters in determining the likelihood of survival to age 100. All four parameters can have important effects on the conclusions emerging from this sort of analysis, although it may be less obvious why each parameter affects survival probabilities in a given manner. Clearly, increasing values of e₅₀ are associated with increasing probabilities of survival and thus an increasing likelihood of observing an occasional centenarian. For a given level of e₅₀, however, Figures 4, 5, 6 indicate that survival to age 100 is more likely for relatively higher values of ₅m₅₀. This result can be explained as follows: for a fixed value of e₅₀, a higher value of ₅m₅₀ is associated with a slower pace of mortality increase with age, thus yielding a higher probability of survival to very advanced ages.

Similarly, it is also evident that higher values of the background mortality parameter, c, (expressed as a percentage of ₅m₅₀) are associated with a lower probability of survival to age 100. The explanation is somewhat complicated: a higher level of background mortality around age 50 implies a lower level of senescent mortality; above age 50 in this situation, senescent mortality must increase more rapidly in order to match the fixed level of e₅₀, thus yielding a more pronounced die-off at older ages and thus a lower probability of survival to advanced ages. Thus, as seen in Figures 4-6, the likelihood of observing an occasional centenarian diminishes considerably as c increases from 5 to 65 percent of ₅m₅₀. Typically, the value of c as a percent of ₅m₅₀ declines as mortality levels drop and life expectancy increases. Thus, the fourth graph in each figure, where c is derived from an OLS regression of c on e₅₀ and ₅m₅₀, is more similar to the graph marked "c = 65%" at low levels of e₅₀ and to the graph marked "c = 5%" at high levels of e₅₀.

The importance of the fourth parameter, n, is also evident in Figures 4, 5, 6. Since 1/n equals the upper asymptote of the age curve of mortality, higher values of n are associated with lower mortality rates at high ages and thus higher probabilities of survival to advanced ages. For this reason, the dots in Figures 4, 5, 6 are most often present in the fourth column of each cluster (corresponding to n = 1.5) and most often absent in the first column ( n = 0).

In all three time periods examined in Figures 4, 5, 6, it is evident that life expectancies (e₅₀) at the low end of the range considered here imply mortality conditions that could have been too harsh to guarantee at least one centenarian per century. At the other extreme, a relatively high value of e₅₀ within this range suggests mortality conditions that would have yielded at least one centenarian per century in almost every conceivable scenario. In between these two extremes, it is difficult to reach any firm conclusions about whether or not there may have been occasional centenarians during these time periods. To develop this discussion further, however, we first need some standard about how to evaluate the information in these figures.

Note that it is possible to have a maximum of 28 dots in these figures for each combination of e₅₀ with a given method of deriving c, the background mortality parameter. If all 28 dots are present, we may conclude that an occasional centenarian was extremely likely (i.e., with a probability greater than 0.99) under every plausible mortality scenario at that level of mortality and for that choice of c. If we narrow our focus to the overall mortality level, e₅₀, then there are a total of 4 x 28 = 112 possible dots. Note in Figure 6, for example, that only 5 of these 112 possible dots are missing when e₅₀ equals 19. At the other extreme, there are only 50 dots present (thus, less than half) in these graphs when e₅₀ equals 9. If we consider that all of these scenarios are equally likely (surely not the case, but a useful simplification for our current purposes), we have a quantitative means of asserting that assumed levels of e₅₀ around 19 suggest that there would almost certainly have been at least one centenarian during the 17th century, while levels around 9 indicate that the existence of a single centenarian in this period would have been a possibility although by no means a certainty.

In the middle range of e₅₀, any conclusion about the likelihood of an occasional centenarian depends critically on the assumed values of the other parameters of the mortality model and on population size as well. When e₅₀ equals 14, for example, the three figures contain a total of 63, 89, or 90 dots out of the 112 possible (corresponding to the periods around 8000 B.C., A.D. 0-14, and the 17th century, respectively). Thus, for the latter two periods, mortality levels in the middle range would yield an occasional centenarian in more than three fourths of the plausible mortality scenarios. For the earliest time period, however, only about half of the plausible scenarios at this level of e₅₀ would produce an occasional centenarian. Therefore, we might reasonably conclude that an e₅₀ around 14 years would provide a fairly strong indication (though no guarantee) of occasional centenarians from at least Roman times to the present. In earlier time periods with much smaller population sizes, such as those probably observed at the dawn of the agricultural era, it seems almost equally likely from our vantage point that an e₅₀ around 14 years might have yielded at least one centenarian per century, or that centenarians could have been rarer or even non-existent.

In a previous section, we have argued that a life expectancy, e₅₀, around 14 years is a reasonable "best guess" based on available evidence of mortality levels prior to the industrial era. If this estimate is accurate, we might wish to identify more precisely the first time period in which there is a strong indication that there would have been at least an occasional living centenarian. Based on the preceding analysis, we may attempt to identify a population size and corresponding time period where three fourths of the mortality scenarios associated with an e₅₀ of 14 years indicate the presence of an occasional centenarian with very high probability. By trial and error, it was determined that a world population of just under 100 million persons would be sufficient to produce such a result. Using Durand's population estimates (see Table 3) and assuming a fairly stable growth rate between 8000 B.C. and A.D. 0-14, such a population size would have been attained sometime during 3000-2000 B.C., thus around the time of the nascent civilizations of the ancient world (for example, the Old Kingdom in Egypt, or the Sumerian era in Mesopotamia).⁶

Arguably, then, centenarians may have been a product, not of industrialization during the past 200 years, but of civilization during the past 5000 years. It was not the trappings of civilization per se, however, that would have yielded an increase in the likelihood of observing an occasional centenarian, since there is no evidence that the rise of early civilizations resulted in a reduction in levels of morbidity or mortality, or a corresponding increase in life expectancy (Cohen 1989). Rather, it was the slow growth of world population during this period that accounts for the increasing probability that at least one individual would have attained this milestone age during the course of a single century. It must therefore be considered coincidental that the critical population mass necessary to yield an occasional centenarian at the assumed mortality level (e₅₀ around 14 years) was attained around the time of the birth of civilization.

Our earlier analysis has shown that, under plausible mortality assumptions, at least an occasional individual must have survived to the age of 100 years since the beginnings of civilization some 4000-5000 years ago. Another approach to this problem is to estimate the prevalence of centenarians in a stable population under a range of assumptions. Using this approach, we specify an a prior distribution for each parameter of the mortality model, and then calculate prevalence estimates by drawing randomly from those distributions. The result is a distribution of estimates of centenarian prevalence. The center of that distribution may be taken as our best estimate of centenarian prevalence, and the sensitivity of that center to changes in the underlying assumptions can be assessed.

According to stable population theory (e.g., Keyfitz 1985), the proportion of the population above age 100 is as follows:

where x in these integrals denotes age, b (in this equation only) is the birth rate, r is the population growth rate, l(x) is the probability of survival from age 0 to x, and y is some intermediate age (in our example, age 50) such that precise mortality estimates are available only above age y. The complication of splitting the integral in the denominator at age y is necessitated by the fact that our parametric mortality model is valid for adult ages only. For convenience, we choose y = 50.

Lacking estimates of l(x) for x<y, it is necessary to approximate the first integral of the denominator. Assuming a linear decline in the survival curve from age 0 to y, i.e.,

it is possible to show that

Using these formulas, we can calculate the prevalence of centenarians in the stable population, _Ąc₁₀₀, given three quantities: 1) the probability of surviving from age y to x, l(x) / l(y), for all x > y; 2) the probability of surviving from birth to age y, l(y); and 3) the population growth rate, r.

The values of the parameters in equation (6) were selected in a manner that reflects our uncertainty about their true values during the pre-industrial period. The result is a set of simulations where the exact values of the chosen parameters are different for each trial. First, a set of simulations were performed using a "base model". Next, various modifications to the base model were made and additional sets of simulations were computed in order to evaluate the sensitivity of the results to changes in assumptions.

For each trial, the choice of parameters for the base model can be described briefly as follows:

1.	e₅₀ was fixed at 14 years.
2.	₅m₅₀, c, and l(50) were drawn at random from normal distributions whose means were chosen conditionally based on all previously selected parameters. (In other words, using the same set of high-mortality model life tables as before, the distribution for ₅m₅₀ was centered on the predicted value from a simple regression on e₅₀; the distribution for c was centered on the predicted value from a multiple regression on e₅₀ and ₅m₅₀; and the distribution for l(50) was centered on the predicted value from a multiple regression on e₅₀, ₅m₅₀, and c.) In each case, the standard error for this distribution was set equal to the maximum residual (from the respective regressions) divided by 3.
3.	n was drawn at random from a normal distribution centered on 1.0, with a standard error of 0.2.
4.	The population growth rate, r, was fixed at 0.05%, which equals the long-term annual growth rate of the human population during the agricultural era. (The population growth rate was not allowed to vary within each set of simulations since we can be more certain about its value, at least in the long term, than about the parameters of the mortality model.)

After choosing the parameters for each simulation trial, equation (6) was used to compute the prevalence of centenarians, expressed as a proportion of the total (stable) population. The resulting distribution of prevalence estimates is shown in Figure 7. It is evident that these estimates have a wide range, reflecting the uncertainty about centenarian prevalence that results from our uncertainty about the relationships between the various parameters of the mortality model. After a logarithmic (base 10) transform, however, the distribution of prevalence estimates has a nearly symmetrical shape. The median prevalence estimate in the base model, as reported in Table 4, is 4.7 centenarians per 100 million population. Expressed as a base-10 logarithm, the median estimate equals -7.33 and thus lies squarely in the middle of the distribution shown in Figure 7. Although the entire distribution has a rather broad range, over three fourths of these prevalence estimates are above 1 per 100 million (or 10^-8).

These results provide further (and stronger) support for our earlier conclusion that centenarians must have been observed at least on occasion once world population surpassed 100 million. By our previous arguments, with e₅₀ equal to 14 years, around three quarters of the plausible mortality scenarios yielded a high probability of observing at least one centenarian every hundred years once world population exceeded 100 million. Now, over three fourths of our plausible mortality scenarios (with e₅₀ fixed at 14 years, accompanied by various age patterns of mortality) predict an average of at least one centenarian at any given moment out of a population of 100 million.

Table 4 also gives prevalence estimates for super-centenarians (individuals aged 110 years or older) derived from the simulations of the base model. These results suggest unmistakably that no individual was likely to have survived to age 110 during the agricultural era. The median estimate for the prevalence of super-centenarians in this model is 0.002 per 100 million. At this level, a population of 100 million persons observed for 1000 years would have only an expected 2 person-years of super-centenarian lifetime. Such a small expectation can reasonably be equated with our everyday notion of impossibility. Only the most optimistic 10-15 percent of the simulated mortality scenarios produce estimates of super- centenarian prevalence that might contradict the conclusion that there were no individuals living past age 110 during the agricultural era. Thus, although there may have been occasional centenarians for the past 4 or 5 thousand years, it appears that super-centenarians were most likely a product of the mortality decline of the industrial era.

The sensitivity of the centenarian prevalence estimates is evaluated in Table 5. This analysis varies the levels of mortality (e₅₀) as well as the other parameters of the mortality model (₅m₅₀, c, and n). In the former case, four additional (fixed) values of e₅₀ are employed. In the latter three cases, the distributions of the simulated parameters are increased or decreased by one standard error relative to the base model.

Another sensitivity test varies the size of the standard error (s) used in the simulations. In the base model, the standard error used for deriving ₅m₅₀, c, and l(50) equalled the maximum residual (from each regression) divided by 3. For a sensitivity analysis, a smaller s was obtained by dividing by 4; a larger s, by 2. Two other modifications to the base model were the "wild card l(50)" and variations in the population growth rate, r. For the "wild card l(50)" trial, the simulations were modified to include an occasional choice for l(50) that was unusually high given the levels of e₅₀, ₅m₅₀, and c (to mimic the Far Eastern mortality pattern, which was dropped from the earlier regression model of l(50)).⁷

Most of these changes yielded results that would not materially alter our conclusions regarding the prevalence of centenarians in pre-industrial times: for most scenarios, nearly three quarters or more of the simulations predict at least one centenarian per 100 million population. One exception to this rule is the scenario with a growth rate of 2 percent. Sustained growth rates of this magnitude in pre-industrial times must be considered very unlikely, however, so we need not be overly concerned with this result. On the other hand, it is important to examine the effects of altering the overall level of mortality (e₅₀) or the conditional distribution of ₅m₅₀ (given e₅₀).

In each of the simulations, the level of ₅m₅₀ was derived from a regression model (with e₅₀ as the independent variable). It is clear from Table 5 that a shift of one standard error in the conditional distribution of ₅m₅₀ has a relatively larger impact on the distribution of prevalence estimates than the other sensitivity tests, with the exception of changes in the mortality level itself (i.e., e₅₀). Nevertheless, these sensitivity tests would not alter the most important conclusion of this analysis, namely, that the expected prevalence of centenarians worldwide exceeded one well before the industrial era. Even in the scenario labeled "Lower ₅m₅₀", three quarters of the scenarios have prevalence estimates above 0.35 per 100 million. Thus, at least one centenarian would be expected in a population of 300 million or more, which was achieved during Roman times. At the other extreme, the "Higher ₅m₅₀" scenario suggests that a population much smaller than 100 million might have contained at least one centenarian (on average). It is difficult to argue that these scenarios are extremely unlikely: the centers of the (conditional) distributions of ₅m₅₀ differ from the regression model by one standard error, which is only one third of the maximum residual from the regression. Thus, there remains a degree of uncertainty about the precise timing of the emergence of centenarians, although we can remain fairly certain that the emergence (by this definition) preceded the industrial era by nearly 2000 years or more.

Obviously, it is the overall mortality level that has the largest impact on our predictions regarding the prevalence of centenarians through history. If late adult mortality was lower (e₅₀ equal to 16 or 18 rather than 14 years), we might expect to see centenarians at much smaller population sizes: with more than three fourths of the prevalence estimates above 1 per 10 million, we might predict that centenarians have existed almost since the dawn of the agricultural period some 10,000 years ago. On the other hand, if late adult mortality was higher (e₅₀ of 10 or 12 years), we would have difficulty claiming that the emergence of centenarians occurred prior to the mortality decline of the industrial era. Our basis for believing that agricultural e₅₀ was centered around 14 years was presented in the preceding section and will not be repeated here. It is obvious, however, that the strength of our conclusions regarding the timing of the emergence of centenarians depends critically on this assumption.

It is possible, of course, that the reality may be a mixture of the mortality scenarios we have presented here. Undoubtedly, different populations living at the same moment experienced different mortality conditions, due to variations in diet, environment, and exposure to disease. This chapter essentially ignores these spatial variations and considers what the average mortality level of the entire world population might have been. Given the absence of detailed information, this strategy seems to be a useful simplification. There appear to be no obvious theoretical reasons for worrying about the effects of heterogeneous mortality patterns on our conclusions. A more thorough investigation of this topic would perhaps be warranted but is beyond the scope of this study.

Another form of variation in mortality patterns that we have thus far dismissed may also deserve more careful consideration. Although we have argued that there is no clear evidence of a long-term temporal trend in mortality levels during the agricultural era, it seems prudent to entertain at least the possibility of such a change. For example, if there was a gradual increase in late adult life expectancies (e.g., e₅₀) during this period, then the gradual emergence of centenarians in the population might be attributed to both decreasing mortality and increasing population size. Contemplating this scenario, we might wish to restate our main conclusions regarding occasional centenarians or prevalence levels for centenarians in the population. In each case, we would define a cut-off point in terms of both a mortality level and a population size where we would expect to find some minimal level of centenarians. Using our earlier criteria (a preponderance of evidence that there would have been at least one centenarian per century, or an average of at least one living centenarian at any given time), we would seek a combination of e₅₀ and total population size that would give positive indications of the emergence of centenarians. Based on the evidence presented here, one combination that would work would be an e₅₀ around 14 years or greater and a population size of at least 100 million. Decreases in e₅₀ would need to be associated with very large increases in population size: for example, an e₅₀ around 12 years would require a population size of over 1 billion people in order to indicate the emergence of centenarians by either of our two criteria.

Finally, we may note that the two criteria for the emergence of centenarians that we have examined may seem to be rather different, and yet they produce very similar results. For example, it is obvious that a prevalence estimate indicating an expectation of one or more living centenarians at all times is a stricter requirement than a very high probability of observing at least one centenarian per century. The relationship between the two criteria is not simple, however: an expectation of one centenarian per year (on average) is by no means a guarantee of one centenarian in each single-year cohort. In fact, we know that this expectation must be around 5 or more in order to observe at least one centenarian with virtual certainty. Thus, the strictness of the two criteria differs, in some sense, by a factor of around 20, not by a factor of 100.

Why, then, do the two criteria yield similar results, if in fact one criterion is 20 times more difficult to achieve than the other? The answer lies in the operationalization of the two criteria. In effect, because it was more amenable to a simulation exercise, the prevalence criterion received a more careful operationalization. The occasional centenarian method examined a very broad range of parameters, some of which stretch the limits of plausibility, and sometimes gave equal weight to parameter choices that were not equally likely. In particular, our operationalization of the occasional centenarian method included consideration of a model assuming exponential increase in the age pattern of mortality ( n = 0). In our quantitative summaries, we gave equal weight to this scenario, although it can not be considered equally likely based on available evidence. This choice, in particular, had the effect of making the occasional centenarian criterion more strict, thus yielding results that are similar in character to the prevalence criterion. It would of course be possible to operationalize the occasional centenarians criterion using a simulation model, but we have chosen to present the results of this method in their current form because they are informative in a different way. So presented, the results help us to understand the importance of each parameter in the mortality model. In terms of our final results, however, it is better to rely on the conclusions of the prevalence model.

1.	Reliable records of centenarians in pre-industrial populations are not widely available. Therefore, statistical models are a useful tool for determining whether it is likely that some centenarians may have lived during the agricultural era.
2.	There is no conclusive evidence of major long-term changes in human mortality levels prior to about 1600 A.D. Through most of human history, life expectancy at birth, e₀, appears to have been centered in the low to mid twenties, perhaps around 24 years. Life expectancy at age 50, e₅₀, is thought to have averaged around 14 years. These conclusions are based both on a wide range of direct evidence (see Table 1) and on two collections of model life tables (Coale-Demeny 1983, Preston et al. 1993).
3.	Centenarians remain a rarity even in modern, low-mortality populations, with an estimated prevalence around 50-100 per million.⁸ Thus, statements claiming that "centenarians were very rare prior to industrialization" do not distinguish modern from pre-modern mortality regimes in a meaningful way.
4.	Nevertheless, it is possible to define arbitrary criteria that allow us to estimate the timing of the "emergence of centenarians." Two criteria of emergence are proposed here: 1) virtual certainty (p ł 0.99) of at least one centenarian per century, and 2) a prevalence estimate that implies at least one living centenarian (on average) at any time. In both cases we examine a variety of plausible mortality scenarios and claim evidence of emergence if and only if a preponderance of evidence (three quarters of the scenarios) is consistent with such a conclusion.
5.	Using the prevalence criterion, our best estimate indicates that the emergence of centenarians should have occurred by around 2500 B.C. in a world population of some 100 million persons. Thus, this emergence probably occurred during the time of the first great human civilizations (e.g., the Old Kingdom in Egypt, the Sumerian period in Mesopotamia). This conclusion, however, is very sensitive to our assumption about the average level of e₅₀ in the pre-industrial period. Although our evaluation of the available evidence leads us to the conclusions stated here, if e₅₀ was in fact nearer to 12 than to 14 years throughout this period, then Jeune's hypothesis that there were no true centenarians prior to 1800 may be closer to the truth.
6.	Finally, although we believe that the emergence of centenarians probably occurred well before the industrial era, our analysis provides rather strong support for the assertion that there were almost certainly no true super-centenarians (individuals aged 110 or above) prior to the mortality decline of the past 200-300 years.

___________________

¹Formally, this conversion ought to include some requirement about choosing "compatible" e₅₀ and ₅m₅₀, so that a and b do not come out to be zero or negative. There probably is no easy analytical description of the boundary conditions for this choice, since formulas for life table functions more complicated than l(x) do not exist for the curves in the Gompertz-Perks family. We have not investigated this issue in detail, but it seems likely to be irrelevant to the present study, which is limited to mortality curves that are in most aspects derived from families of model life tables.

___________________

²Although note that, since the estimates of e₅₀ for the Wang are around 16-18 years, this would be an advantaged mortality experience even if average values were as high as 14 years.

___________________

³Detailed data for the new model life tables by Preston et al (1993) became available to us after the computational analyses of this paper were complete. Due to time constraints, it was not possible to re-compute the regression equations and subsequent simulations including these new tables, which have the advantage of being derived from an interpolation within the range, rather than an extrapolation outside the range, of actual data. It seems unlikely, however, that their inclusion would have changed our results substantially.

___________________

⁴An alternative method would have been to choose a range of values for log (₅m₅₀) based on multiples of the root mean-squared-error of the regression. If the observations were independent, there would be an elegant statistical theory to support such a choice. In this situation, however, the observations are clearly dependent, so there is no strong rationale for using this technique.

___________________

⁵Values of c were estimated by fitting the Perks formula to model life table ₅m_x values (above age 50 only) using the method of maximum likelihood.

___________________

⁶It is worth noting that the estimates of historical population size by Biraben (1979) suggest that a world population of 100 million may have first been achieved somewhat later, around 1200 B.C. The paucity of reliable data about world population size in this period requires that we acknowledge the uncertainty of our estimated date for the emergence of centenarians, although it does not seem obligatory that we revise our best estimate based on the difference between Biraben's and Durand's figures.

___________________

⁷With a probability of 95 percent, l(50) was drawn by the method of the base model. With a probability of 5 percent, the predicted value of l(50) from the regression of the base model was increased by 0.2 (while retaining the same standard error)

___________________

⁸For example, Labat and Dekneudt (1989) estimate that there were 3000 centenarians in France in 1988. Thus, in one of the world's most aged populations, numbering around 57 million, there are some 52 centenarians per million population. Similarly, there were an estimated 25,000 centenarians in the United States during 1985 (U.S. Bureau of Census 1987). In a population of some 240 million, this corresponds to a frequency slightly greater than 100 per million. Since the French population is generally more aged than the U.S. population (for example, in terms of the proportion above age 65), we should expect a higher proportion of centenarians in France than in the U.S. Although the U.S. figure is derived from Social Security records, it may still be biased upwards by age exaggeration (Coale and Kisker 1990).